初中物理杠杆的平衡条件试题

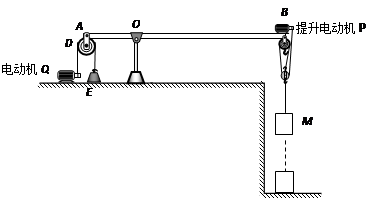
如图甲所示，B是一个固定支架，由立柱和两侧装有定滑轮的水平横梁组成，物体M在横梁上可左右移动，M的左端用钢绳跨过定滑轮与电动机相连，右端用钢绳跨过定滑轮与滑轮组相连，滑轮组下挂一实心物体A，其密度ρ_Ａ=5×10³kg/m³，体积V_A=0.024m³。当电动机不工作时（可视电动机对钢绳无拉力作用），将物体A浸没在水中，物体A可以通过滑轮组拉着物体M向右匀速运动；当电动机用一个竖直向下的力F₁拉钢绳时，物体A在水面下以速度υ₁=0.1m/s匀速上升，滑轮组的机械效率为η₁；当物体A完全露出水面后，电动机用力F₂拉钢绳，物体A匀速上升，滑轮组的机械效率为η₂。在以上过程中，电动机对钢绳的拉力的大小随物体A上升高度的关系如图乙所示，电动机以F₁、F₂拉钢绳时的功率始终为P。（不计钢绳的质量、滑轮与轴的摩擦、水对物体的阻力。取g =10N/kg）

求：
（1）滑轮组的机械效率η₁：η₂
（2）电动机的功率P

如图所示，有两个小球M和N，密度分别为ρ_M和ρ_N，小球所受重力大小分别为G_M和G_N，体积分别为V_M和V_N。将它们用细线分别挂在轻质杠杆AB两端，且小球M浸没在甲杯的水中静止，小球N浸没在乙杯的油中静止，杠杆AB恰能在水平位置平衡。小球M和N所受浮力分别为F_M和F_N。已知：AO׃OB =1׃2，水的密度为ρ_水、油的密度为ρ_水，且ρ_N＞ρ_M＞ρ_水＞ρ_油，则下列判断中正确的是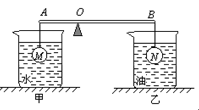

A．FM＜2FN

B．FM＞2FN

C．VM＞2VN

D．GM＞2GN

用如图（1）所示的装置提升重物，水平横梁AB 固定在支架C顶端，OA： OB=4：1。横梁A端挂一底面积为S=0.1m²的配重M，横梁B端下挂着由质量相等的四个滑轮组成的滑轮组，用此滑轮组多次提升不同的物体，计算出滑轮组的机械效率，并记入下面的表格。

物重G/N	60	80	100	180
机械效率η	0.75	0.80	0.833	0. 90

 

现用滑轮组分别提升甲、乙两个物体：在水面以上提升密度为ρ_甲=0.75kg/dm³的甲物体时，绳自由端的拉力为F₁，F₁做的功为W₁，配重M对地面的压强变化量为ΔP₁；在水面以下提升密度为ρ_乙=5.6kg/dm³的乙物体时，绳自由端的拉力为F₂，F₂做的功为W₂，配重M对地面的压强变化量ΔP₂。
F₁、F₂所做的功随时间变化的关系如图（2）所示。已知：甲、乙两物体的体积关系为V_甲=4V_乙，提升甲、乙两物体时速度相同。（不计绳的质量、杠杆的质量、轮与轴的摩擦、水对物体的阻力。取g =10N/kg）求：
（1）配重M对地面的压强变化量的差ΔP₂－ΔP₁
（2）滑轮组提升浸没在水中的乙物体时的机械效率。（保留百分号前面一位小数）

如图所示为一种蓄水箱的放水装置，AOB是以O点为转轴的轻质杠杆，AO呈水平状态，如图A、O两点间距离为40cm， B、O两点间距离为20cm，且OB与水平面夹角为60°。A点正下方的Q是一个轻质、横截面积为100cm²的盖板（盖板恰好能堵住出水口），它通过细绳与杠杆的A端相连。在水箱右侧的水平工作台上，有一质量为60kg的人通过滑轮组拉动系在B点呈竖直状态的绳子，从而可以控制水是否能从出水口流出。若水箱中水深为50cm，当盖板恰好要被拉起时，人对绳子的拉力为F₁，工作台对人的支持力为N₁；若水箱中水深为100cm，当盖板恰好要被拉起时，人对绳子的拉力为F₂，工作台对人的支持力为N₂。已知N₁与N₂之比为9：7，盖板的厚度、绳重及滑轮的摩擦均可忽略不计，人对绳的拉力与人所受重力在同一直线上，取g=10N/kg。求：

（1）动滑轮所受的重力
（2）F₁：F₂
（3）当水位至少达到多高时，人无法拉起盖板。

如图所示，在底面积为50cm²的大烧杯中装有适量的水，杠杆CD可绕支点O在竖直平面内转动，CO=3DO，钩码A的质量为100g。杠杆CD在水平位置平衡时，物体B有的体积露出水面；当在A的下方加挂１个相同的钩码时，物体Ｂ有的体积露出水面，杠杆CD仍在水平位置平衡。g取10N/kg，杠杆、悬挂物体的细绳的质量可忽略不计，则下列选项正确的是  

A．物体B的密度1.5×10^3kg/m^3

B．物体B的体积为500cm^3

C．物体B浸没在水中受到浮力的大小为75N

D．挂两个钩码与挂一个钩码相比，烧杯底部受到水的压强减小了600Pa

如图所示，杠杆AB的A点挂边长为2dm、密度为ρ₁=2kg/dm³的正方体C，B点挂边长为1dm正方体D，AO:OB=2:5，杠杆在水平位置平衡时，D静止在空中，C对水平地面的压强为p₁=1000Pa；若将正方体D浸没在某种液体中（未接触到容器底），杠杆在水平位置平衡时，C对水平地面的压强增大了1250Pa，取g=10N/kg，可求得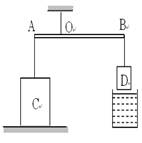

A．物块D的密度为5kg/dm^3

B．液体的密度为2kg/dm^3

C．当物体D浸没在液体中时A点所受竖直向下的拉力为95N

D．若物体D不浸入液体，要使物体C对地面的压强为零，则应对物体D施加竖直向下的64N的力

如图是锅炉安全阀示意图、阀的横截面积S为4厘米²，OA∶AB=1∶2，若锅炉能承受的最大压强为5.4×10⁵帕，在B处应挂多重的物体G？若锅炉能承受的最大压强减小，为保证锅炉的安全，应将重物向什么方向移动？　

一架不准确的天平，主要原因是横梁左右两臂不等长。为了减少实验误差，先把物体放在左盘称得质量为m₁，再把物体放在右盘称得质量为m₂，该物体的真实质量为[　]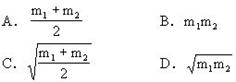

某人将一根木棒的一端抬起，另上端搁在地上。在抬起的过程中（棒竖直时除外），所用的力始终竖直向上，则用力的大小　　[　]

A．保持不变	B．逐渐增大
C．逐渐减小	D．先减小后增大

如图所示，AO=40厘米，BO=20厘米，拉力F=3牛，并与水平方向成30°角。若在木棒B端悬挂体积为100厘米³的物体G，并将它浸没在水中，木棒恰好平衡，则物体的重力应为[　]

A．3牛	B．4牛
C．6牛	D．6.98牛

如图，杠杆每小格的长度相等，质量不计，以O为支点，杠杆的右端挂有重物M，支点左边的A处挂钩码时，杠杆平衡，将重物M浸没在水中，钩码放在B处，杠杆又平衡，则重物与钩码的质量之比为      ，重物M的密度是        kg/m^3．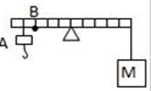

一根杠杆两端挂有等重的实心铜块和铁块,当它们都浸没在水中时,杠杆恰好平衡,现将铜块和铁块同时从水中取出,则杠杆将(    )

A．铜块端向下运动	B．铁块端向下运动
C．杠杆仍然平衡	D．条件不足,无法判断

示轻质杠杆，把密度均为4.0×10³kg/m³的甲、乙两个实心物体挂在A、B两端时，杠杆在水平位置平衡，若将甲物体浸没在水中，同时把支点从O移到O′时，杠杆又在新的位置平衡，若两次支点的距离O O′为OA的，求：甲、乙两个物体的质量之比．

图1—5—19

如图13-4-4所示，等臂杠杆两端各挂一个质量相等的实心铁块和铝块（已知ρ_铁＞ρ_铝），杠杆平衡，若将它们同时浸没在水中，杠杆将（　　）

图13-4-4

A．仍平衡

B．左端下沉

C．右端下沉

D．无法判定

如图所示，某科技小组的同学制作了一个打捞物体的自动控制模型，E为配重，AOB是一个质地均匀的长方形横杆，其质量不计，OA∶OB=1∶3，在水平位置保持平衡。通过电动机Q可以控制杠杆B端抬起，从而将被打捞物体提起。已知滑轮D重为10N，B端定滑轮和提升电动机P的总质量是1kg，提升电动机P的功率为3W且保持不变，物体M的质量是1kg。只让提升电动机P工作，当物体M匀速上升时，提升电动机P对绳子的拉力为F₁， B端滑轮组的机械效率为η₁。若用质量为1.5kg物体N代替物体M，只让提升电动机P工作，当物体N匀速上升时，提升电动机P对绳子的拉力为F₂， B端滑轮组的机械效率为η₂，且η₁∶η₂=8∶9。不计绳的质量，不计滑轮与轴的摩擦,g取10N/kg，求：
（1）F₁与F₂的比值；
（2）只让提升电动机P工作，当物体M匀速上升时的速度υ；
（3）当物体N被提升到一定高度后，提升电动机P停止工作，启动电动机Q将杠杆B端匀速抬起的过程中，电动机Q对绳子的拉力F的大小。