如图甲所示,在容器底部固定一轻质弹簧,弹簧上端连有一边长为0.1m的正方体物块A,当容器中水的深度为20cm时,物块A有 的体积露出水面,此时弹簧恰好处于自然伸长状态(ρ水=1.0×103kg/m3,g取10N/kg).求:
的体积露出水面,此时弹簧恰好处于自然伸长状态(ρ水=1.0×103kg/m3,g取10N/kg).求:
(1)物块A受到的浮力;
(2)物块A的密度;
(3)往容器缓慢加水(水未溢出)至物块A恰好浸没时水对容器底部压强的增加量△p(整个过程中弹簧受到的拉力跟弹簧的伸长量关系如图乙所示).
图甲是建造大桥时所用的起吊装置示意图,使用电动机和滑轮组(图中未画出)将实心长方体A从江底沿竖直方向匀速吊起,图乙是钢缆绳对A的拉力F1随时间t变化的图像。A完全离开水面后,电动机对绳的拉力F大小为6.25×103N,滑轮组的机械效率为80%。已知A的重力2×104 N,A上升的速度始终为0.1m/s。(不计钢缆绳与滑轮间的摩擦及绳重,不考虑风浪、水流等因素的影响)求:
(1)长方体A未露出水面时受到的浮力;
(2)长方体A的密度;
(3)长方体A完全离开水面后,在上升过程中F的功率。
(4)把长方体A按图21甲中的摆放方式放在岸边的水平地面上,它对地面的压强。
如图所示,弹簧测力计下面挂一实心圆柱休,将圆柱体从盛有水的容器上方离水面某一高度处缓缓下降(其底面始终与水面平行),使其逐渐浸没入水中某一深度处。右图是整个过程中弹簧测力计的示数F与圆柱体下降高度h变化关系的数据图象。已知ρ水=1.0×103kg/m3,g=10N/kg。 
求:(1)圆柱体的重力。
(2)圆柱体浸没时受到的浮力。
(3)圆柱体的密度。
(4)圆柱体在刚浸没时下表面受到的水的压强。
据报道,我市某水库库底是一座旧城遗址,目前正在进行试探性发掘和打捞.某次试探性打捞作业时,用绳子将实心物体从水面下12m 深处沿竖直方向匀速提升到离水面1.5m深处的过程所用时间为42s,拉力F做功的功率为90W.当物体被拉到有4/5的体积露出水面时,让其静止,此时绳子的拉力F'=520N.不计绳子的重力和水的阻力.(水的密度ρ水=1.0×103kg/m3,g="10N/kg" )
求:(1)物体从水面下12m深处匀速上升到离水面1.5m深处的过程中,物体匀速运动的速度v;
(2)物体在水面下方匀速上升过程中绳子的拉力F;
(3)物体浸没在水中时所受的浮力F浮;
(4)物体的密度ρ物.
图甲是某工厂的水平传送带上产品运输及计数器的示意图。S为激光光源,能连续发射粗细忽略不计的激光束;R为光敏电阻,当有激光照射时,其阻值较小,无激光照射时,其阻值较大。每当水平传送带上的产品和传送带一起匀速通过S与R之间时,射向光敏电阻的激光被产品挡住,通过电压表测出光敏电阻R两端电压随时间变化的规律如图乙所示。已知计数器的电源电压为3V,保护电阻R0=200Ω。若水平传送带上的产品均是边长a=0.lm、质量m=2.5kg的实心正方体,求: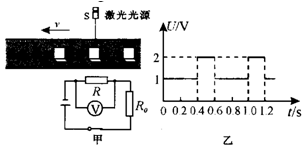
(l)产品的密度;
(2)产品对传送带的压强;
(3)传送带传输产品的速度;
(4)计数器工作1min,光敏电阻R在有激光照射时消耗的电能。
图是液压汽车起重机从水中打捞重物的示意图。A是动滑轮,B是定滑轮,C是卷扬机,D是油缸,E是柱塞。卷扬机转动使钢丝绳带动动滑轮上升,同时提升重物。被打捞的重物体积是 ,若在本次打捞前,起重机对地面的压强 p0=2.0×107Pa,当物体在水中匀速上升时起重机对地面的压强p1=2.375×107Pa,物体全部出水面后起重机对地面的压强p2=2.5×107Pa,假设起重时柱塞沿竖直方向,物体出水前、后柱塞对吊臂的支撑力分别为N1和N2,N1与N2之比为19:24。重物出水后上升的速度
,若在本次打捞前,起重机对地面的压强 p0=2.0×107Pa,当物体在水中匀速上升时起重机对地面的压强p1=2.375×107Pa,物体全部出水面后起重机对地面的压强p2=2.5×107Pa,假设起重时柱塞沿竖直方向,物体出水前、后柱塞对吊臂的支撑力分别为N1和N2,N1与N2之比为19:24。重物出水后上升的速度 ,吊臂、定滑轮、钢丝绳的重以及轮与绳的摩擦不计。(g取10N/kg)求:
,吊臂、定滑轮、钢丝绳的重以及轮与绳的摩擦不计。(g取10N/kg)求:
(1)被打捞物体的密度;
(2)若被打捞物体在水中匀速上升时滑轮组AB 的机械效率为 ,物体全部露出水面在空气中匀速上升时,滑轮组AB 的机械效率为
,物体全部露出水面在空气中匀速上升时,滑轮组AB 的机械效率为 ,求
,求
(3)重物出水后,卷扬机牵引力的功率。
如图甲,在弹簧测力计下挂一圆柱体,从盛水的烧杯上方某一高度缓慢下降,圆柱体浸没后继续下降,直到圆柱体底面与烧杯底部接触为止.如图乙所示的是圆柱体下降过程中弹簧测力计读数F随圆柱体下降高度h的变化图像.试求:(g取10 N/kg)
(1)圆柱体受到的最大浮力.
(2)圆柱体的密度.
将一个容器内装满水后总质量为78g,再往此容器内装入20g沙石后总质量为90g。求:
(1)加入容器内的沙石的体积;(2)沙石的密度。
如图所示,柱形容器中装有密度为ρ1=1.2g/cm3的某种液体,将一金属块放入底面积为S=100cm2的长方体塑料盒中,塑料盒竖直漂浮在液面上,且液体不会溢出容器,其浸入液体的深度为h1=20cm。若把金属块从塑料盒中取出,用细线系在塑料盒的下方,放入该液体中,塑料盒竖直漂浮在液面上,且金属块不接触容器底,塑料盒浸入液体的深度为h2=15cm。剪断细线,金属块沉到容器底部,塑料盒仍竖直漂浮在液面上,其浸入液体的深度为h3=10cm。则金属块的密度ρ2= g/cm3。
在图所示装置中,杠杆和滑轮的重力及滑轮的摩擦均可忽略不计,杠杆AB可以绕O点在竖直平面内自由转动,A端通过竖直方向的轻绳与滑轮组相连,在B端用一轻绳沿竖直方向将杠杆拉住,使其始终保持水平平衡。在滑轮组的下方,悬挂一圆柱形的物体,此物体被浸在圆柱形容器内的液体中。已知杠杆O点两侧的长度关系为AO=2OB,圆柱形物体的底面积为10cm2、高为12 cm,圆柱形容器的底面积为50cm2。若容器中的液体为水,在水深为20cm时物体的上表面恰与水面相平,此时杠杆B端绳上的拉力为F1;打开圆柱形容器下方的阀门K,将水向外释放,直到物体露出水面的体积为其总体积的2/3时,将阀门K关闭,此时杠杆B端绳上的拉力为F2,且F1:F2=3:4。若容器中液体为某种未知液体,其质量与最初容器中的水的质量相等,此时未知液体的深度为18 cm,杠杆B端绳上的拉力为F3。取g=10N/kg,则
| A.圆柱形物体的密度为2 g/cm3 |
| B.作用在B端的拉力F3大小为1.52N |
| C.未知液体的密度为1.2 g/cm3 |
| D.未知液体对圆柱形容器底部的压强为1980Pa |
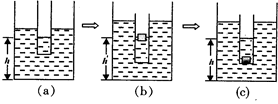
如图 (a)所示,装有部分水的试管竖直漂浮在容器内的水面上,试管内水面与容器底部的距离为h,试管壁粗细均匀、厚度不计;现将某物块放入试管内,物块漂浮在试管内的水面上,试管仍漂浮在容器内的水面上,此时试管内水面与容器底部的距离为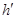 ,如图 (b)所示;取走该物块,将另一物块完全浸没在该试管水中,发现试管内水面与容器底部的距离恰好又变为h,如图 (c)所示,若试管横截面积与容器横截面积之比为1:5,则新放入的物块密度为____
,如图 (b)所示;取走该物块,将另一物块完全浸没在该试管水中,发现试管内水面与容器底部的距离恰好又变为h,如图 (c)所示,若试管横截面积与容器横截面积之比为1:5,则新放入的物块密度为____ 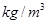 。
。
工人用图所示装置,打捞深井中的边长为30cm的正方体石料,石料的密度为3´103kg/m3。装置的OC、DE、FG三根柱子固定在地面上,AB杆可绕O点转动,AO:OB=1:2,边长为L的正立方体配重M通过绳竖直拉着杆的B端。现用绳子系住石料并挂在滑轮的钩上,工人用力沿竖直方向向下拉绳,使石料以0.2m/s的速度从水中匀速提升。AB杆始终处于水平位置,绳子的质量、轮与轴间的摩擦均不计,g取10N/kg。求:

(1)如果石料在水中匀速上升时滑轮组的机械效率是η1,石料完全离开水面后滑轮组的机械效率是η2,且η1:η2=83:84,求石料在水中匀速上升过程中,工人拉绳的功率多大?
(2)若石料在水中匀速上升时,配重对地面的压强为6500帕,石料完全离开水面后,配重对地面的压强为4812.5帕;求配重M的密度。
如图甲所示的装置处于静止状态,底面积为60cm2的圆柱形玻璃筒中装有适量的水,放在水平台面上,质量为800g的圆柱形物体B浸没在水中,此时水对容器底的压强是2500 Pa,物体A是体积为50cm3的圆柱体配重。如图乙所示,当用力F竖直向下拉物体A时,物体B有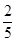 的体积露出水面且静止,此时滑轮组提升重物B的机械效率为80%,水对容器底的压强为2100 Pa。 g取10N/kg,悬挂物体的细绳的质量以及绳与轮间的摩擦忽略不计,物体A的密度是 kg/m3。
的体积露出水面且静止,此时滑轮组提升重物B的机械效率为80%,水对容器底的压强为2100 Pa。 g取10N/kg,悬挂物体的细绳的质量以及绳与轮间的摩擦忽略不计,物体A的密度是 kg/m3。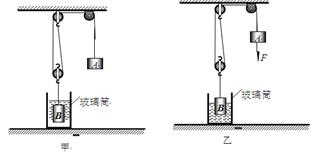
在弹簧测力计下挂一个金属块A,让A从盛有水的容器上方离水面某一高度处匀速下降,进入水中,直到全部浸没。图是这个过程中弹簧测力计的示数F与A下降的高度h变化的实验图象,g=10N/kg。则A的重力为 N,金属块A的密度与下表中 的密度相同。
| 物质名称 |
密度ρ/(kg·m-3) |
| 银 |
10.5×103 |
| 铜 |
8.9×103 |
| 铁 |
7.9×103 |
| 铝 |
2.7×103 |

目前国际上酒的度数表示法有三种,其中一种称为标准酒度,是指在温度为20℃的条件下,每100毫升酒液中所含酒精量的毫升数,中国也使用这种表示法,它是法国著名化学家盖·吕萨克制定的,又称盖·吕萨克酒度.蒸馏出来的酒液需要进行勾兑,勾兑一方面为了保障酒的品质,另一方面可以调整酒的度数,若现有60度和30度的酒液各若干,酒液中的微量元素忽略不计,求:
(1) 60度酒液的密度;
(2)如果用这两种酒液进行勾兑,获得42度、1000 ml的酒液,那么需要这两种酒液各多少毫升。
(已知ρ酒精=0.8×l03 kg/m3,ρ水=1.0×103 kg/m3,不考试酒液混合后体积减小)