已知酒精的密度为0.8×103kg/m3,下列说法能够成立的是 ( )
| A.能装0.5kg纯水的瓶子一定能装下0.6kg的酒精 | B.同体积的水和酒精质量之比是5:4 |
| C.能装下0.5kg酒精的瓶子不能装下0.6kg纯水 | D.同质量的水和酒精体积之比是2:5 |
某同学在测量正方体金属块密度时:
(1)先将天平放在水平工作台上,然后将游码移至横梁标尺的零刻度处。
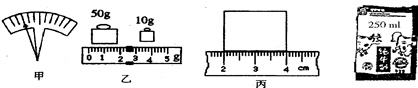
若发现天平指针位置如图甲所示,则应将平衡螺母向 侧调节(填“左”或“右”)。调节天平平衡后,在正确测量的情况下,右盘内所加的砝码和游码在标尺上的位置如图乙所示,则被测金属块的质量为 g。
(2)用刻度尺测量金属块边长情况如图丙所示,则金属块的密度为 kg/m3。
 |
请在下面的数字后面填上适当的单位:
一名中学生的质量约是50______;一个鸡蛋的质量约是60________;8×10-1mL=__________m3;5g/cm3=__________kg/m3。
、在测定液体密度时,某同学测出了液体的体积,容器和液体的总质量,实验共做了三次;记录结果如下表:
| 实验次数 |
① |
② |
③ |
| 液体的体积/cm3 |
16.5 |
35.0 |
40.0 |
| 液体和容器的总质量/g |
21.4 |
39.9 |
m |
(1)该液体密度是 kg/m3;(2)容器的质量是 g.(3)m= g .
、三个完全相同的杯子里装有同样多的水,把质量都为300g的铝块、铁块、铜块分别浸没在这三杯水中(水均未溢出),则水面最高的是(ρ铝<ρ铁<ρ铜) ( )
| A.放入铝块的杯子 | B.放入铁块的杯子 | C.放入铜块的杯子 | D.无法确定 |
已知铅的密度是11.3×103kg/m3,一个实心金属球的体积是0.5dm3,质量是3.9kg,这个金属球的密度是多少?这个金属球是铅做的吗?
小明在实验室里测量一块形状不规则、体积较大的矿石的密度.
(1)用调节好的天平测量矿石的质量.当天平平衡时,右盘中砝码和游码的位置如图所示,矿石的质量是 g.
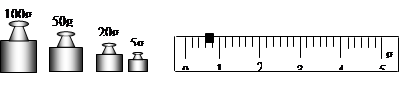 |
(2)因矿石体积较大,放不进量筒,因此他利用一只烧杯,按图所示方法进行测量,矿石的体积是 cm3.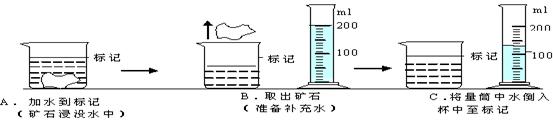
(3)矿石的密度是 kg/m3,从图A到图B的操作引起的密度测量值比真实值 (选填“偏大”、“偏小”、“不变”)
用天平和量筒测定盐水的密度,有如下操作:
| A.用天平称出烧杯和盐水的总质量M; | B.用天平称出烧杯和剩下盐水的总质量m; |
| C.调节天平使天平平衡; | D.将烧杯中的盐水倒入量筒中一部分,记下量筒中盐水体积V; |
(E)用公式ρ=(M-m)/V计算出盐水的密度.
那么,正确操作步骤的序号应是 。
下面列举的语句都蕴含着深刻的哲理,如果从物理学角度来解读,也别有生趣,其中分析不正确的是 ( )
| A.“只要功夫深,铁棒磨成针”,此过程中铁棒的质量减小 |
| B.“蜡炬成灰泪始干”,蜡烛燃烧时的体积减小 |
| C.“锲而不舍,金石可镂”,镂后金石的密度不变 |
| D.“人往高处走,水往低处流”,水流的过程中密度减小 |
下列各物理量中,可用来鉴别物质 的是 ( )
的是 ( )
| A.质量。 | B.密度。 | C.重力。 | D.电阻。 |
、如图1所示表示A、B、C三种物质的质量跟体积的关系,由图可知( )
A.ρA>ρB>ρC , 且ρA>ρ水 B.ρA>ρB>ρC , 且ρA<ρ水
C.ρC>ρB>ρA , 且ρA>ρ水 D.ρC>ρB>ρA , 且ρA<ρ水
为了研究物质某种特性,某同学测得四组数据,填在下列表中:
| 实验次数 |
物体 |
质量/g |
体积/ cm3 |
质量/体积/g·cm-3 |
| 1 |
铝块1 |
54 |
20 |
2.7 |
| 2 |
铝块2 |
108 |
40 |
2.7 |
| 3 |
松木1 |
108 |
216 |
|
| 4 |
松木2 |
10 |
20 |
0.5 |
(1)将上表空格处填写完整.(2)比较第1、2两次实验数据,可得出结论:同一种物质,它的质量跟它的体积成 .(3)比较第2、3两次实验数据,可得出结论:质量相同的不同物质,体积 。(4)比较第1、4两次实验数据,可得出实验结论是 。
、如图1为一盒装纯牛奶.若该牛奶的密度是 1.2×103kg/m3,则牛奶的质量为 kg。喝掉一半后,牛奶的密度将 。(填“变大”、“变小”或“不变”)