甲、乙两金属的密度分别为ρ甲、ρ乙,将等质量的甲、乙两金属制成合金,则合金密度为( )
A. |
B.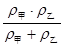 |
C.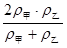 |
D.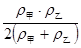 |
如图所示的是A、B两种物质的质量m与体积V的关系图像,由图像可知,A、B两种物质的密度ρA、ρB和水的密度ρ水之间的关系是
A.ρB>ρ水>ρA B.ρB>ρA>ρ水
C.ρA>ρ水>ρB D.ρ水>ρA>ρB
小强同学在探究甲、乙两种物质的质量和体积的关系时,得出了如图所示的图象。由图象分析可知
| A.甲的密度大于乙的密度 | B.甲的密度小于乙的密度 |
| C.甲的密度等于乙的密度 | D.无法比较甲乙 |
在图甲中,石料在钢绳拉力的作用下从水面上方以恒定的速度下降,直至全部没入水中。图乙是钢绳拉力随时间t变化的图像,若不计水的阻力,则可算出该石料的密度为

A 1.6×103kg/m3 B. 2.3×l03 kg/m3 C. 2.8×lO3kg/m3 D.3.2Xl03kg/m3
用量杯盛某种液体,测得液体体积V和液体与量杯共同质量m的关系如图所示,从图中可知( )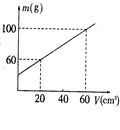
A.该液体的密度是3g /cm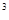 |
B.量杯的质量40g |
| C.体积为60ml时液体质量为100g | D.该液体可能是酒精 |
三个完全相同的杯子里装有同样多的水,把质量都为300g的铝块、铁块、铜块分别浸没在这三杯水中(水均未溢出),则水面最高的是(ρ铝<ρ铁<ρ铜)( )
| A.放入铝块的杯子 | B.放入铁块的杯子 | C.放入铜块的杯子 | D.无法确定 |
王兵在“测量石块的密度”时,测出几组数据,根据这些数据绘出图象,如图6四幅图象中,能正确表示石块“质量与体积的关系”的图象是 ,能正确表示“密度与质量的关系”的图象是 
如图所示表示A、B、C三种物质的质量跟体积的关系,由图可知( )
A.ρA>ρB>ρC , 且ρA>ρ水 B.ρA>ρB>ρC , 且ρA<ρ水
C.ρC>ρB>ρA , 且ρA>ρ水 D.ρC>ρB>ρA , 且ρA<ρ水
甲、乙、丙三个相同柱状容器内分别盛有质量相等的不同液体,将质量相等的实心铜、铁、铝球(已知ρ铜>ρ铁>ρ铝)分别浸没在液体中,此时液面等高,则液体对容器底的压强( )
| A.p甲<p乙<p丙 | B.p甲=p乙=p丙 | C.p甲>p乙>p丙 | D.p甲=p乙>p丙 |
如图,是A、B、C 三种物质的质量m与体积V的关系图线,由图可知,A、B、C三种物质的密度 、
、 、
、 和水的密度
和水的密度 之间的关系是 ( )
之间的关系是 ( )
A. >
> >
> ,且
,且 >
> B.
B. >
> >
> ,且
,且 >
>
C. <
< <
< ,且
,且 <
< D.
D. <
< <
< ,且
,且 <
<
三个完全相同的杯子里面装有水,把质量相同的实心铜块、铁块、铝块(密度大小关系见密度表)依次放在甲、乙、丙三个杯子中,水面恰好相平,原来装水最多的杯子是 ( )
| A.甲杯 | B.乙杯 | C.丙杯 | D.原来装水一样 |
体积相同的铜、铁、铝、木四个小球,放人水中静止后如图所示,其中铝球对容器底部有压力。已知这几种物质的密度关系是ρ铜>ρ铁>ρ铝>ρ木,则下列判断 正确的是()
| A.铝、木两球一定是实心的,铜、铁两球一定是空心的 |
| B.铜、铁两球一定是空心的, 铝、木两球也有可能是实心的 |
| C.四个小球的重力关系是F铁=F铝>F木>F铜 |
| D.四个小球所受浮力关系是F铜>F铁>F铝>F木 |
电流是看不见的,我们在研究它的时候,往往是通过观察它产生的效应来了解它的。如在电路中接一只灯泡,观察灯泡亮度变化就可以知道电流大小的变化,这种方法在科学探究中叫转换法。下面哪个实验也用了这种方法( )
| A.将电流类比水流 | B.保持压力不变,改变受力面积,观察压力的效果 |
| C.用温度计显示物体的温度 | D.用一条带箭头的线段表示力 |
300年前,意大利科学家做了这样一个实验:在房间里挂了许多铃铛,然后
让蝙蝠在房间中自由飞。第一次未对蝙蝠有任何限制,铃铛未响;第二次蒙住
蝙蝠的眼睛,铃铛也未响;第三次塞住蝙蝠的耳朵,房间中的铃铛响了。下列问题不是该实验所研究的是
| A.蝙蝠飞行是靠什么躲避障碍物的 |
| B.眼睛对蝙蝠飞行是否起作用 |
| C.耳朵对蝙蝠飞行是否起作用 |
| D.铃铛是怎样发声的 |