初中数学一次函数的最值试题

某私营玩具厂招工广告称：“本厂工人工作时间：每天工作8小时，每月工作25天；待遇：熟练工人按计件付工资，多劳多得，且计件工资不少于1000元时，每月另加福利工资100元，按月结算……”．  该厂只生产两种玩具：小狗和小汽车，熟练工人晓凤一月份领工资1145元，她记录了如下一些数据：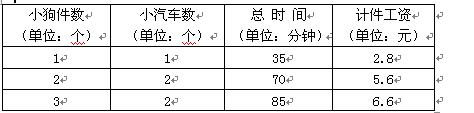

根据表格中的信息，试求出做1个小汽车所需时间和计件工资各是多少?
设晓凤某月生产小狗x个，小汽车y个，月工资(计件工资+福利工资=月工资)为W元．试求W与x的函数关系式.(不需写出自变量x的取值范围)
有一天，厂方从销量方面考虑，对生产作了调整：每个工人每月生产小狗的个数不少于生产小汽车个数的2倍，假设晓凤的工作效率不变，且服从厂家安排，请运用数学知识说明厂家招工广告是否有欺诈行为．

下列函数中，其图象同时满足两个条件①у随着χ的增大而增大?；②与?轴的正半轴
相交，则它的解析式为（  ）

A．у=-2χ-1

B．у="-2χ+1"

C．у=2χ-1

D．у=2χ+1

已知函数的图象如图，则的图象可能是（ ）

．如图所示的计算程序中，y与x之间的函数关系所对应的图象应为（   ）

取相反数

×2

＋4

已知点（-2，y1），（-1，y2），（1，y3）都在直线y=－3x+b上，则y1，y2，y3的值的大小关系是（    ）

A．y1>y2>y3

B．y1<y2<y3

C．y3>y1>y2

D．y3<y1<y2

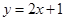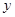已知一次函数，则随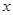的增大而_______________（填“增大”或“减小”）．

一次函数的图象经过点（1，2），且y随x的增大而减小，则这个函数的解析式可以是                .（任写出一个符合题意即可）

如果直线经过第一、二、三象限,那么____0．

若函数y＝2x＋b经过点(1，3)，则b＝ _________．

已知一次函数的图象经过点，，则      ，      ．

已知：2x-3y=1，若把看成的函数，则可以表示为

函数：①y=；②y=；③y=④y= ；⑤y= ；⑥y=0.5x中，属一次函数的有                   。（只填序号）

在同一直角坐标系中，一次函数y=ax+b和二次函数y=ax²+bx
的图像可能为（　　）A

函数：①y=；②y=；③y=④y= ；⑤y= ；⑥y=0.5x中，属一次函数的有                  。（只填序号）

若函数y＝kx+b的图像经过点（－3，－2）和（1，6）求k、b及函数关系式。