初中数学二次函数在给定区间上的最值选择题

根据下表中的二次函数的自变量与函数的对应值，可判断该二次函数的图象与轴（    ）．

A．只有一个交点	B．有两个交点，且它们分别在轴两侧
C．有两个交点，且它们均在轴同侧	D．无交点

已知二次函数的图象（﹣0．7≤x≤2）如图所示、关于该函数在所给自变量x的取值范围内，下列说法正确的是（ ）

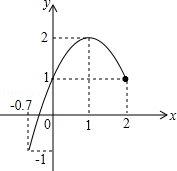
A．有最小值1，有最大值2

B．有最小值-1，有最大值1

C．有最小值-1，有最大值2

D．有最小值-1，无最大值

下列命题：在二次函数y=ax²+bx+c中
①若，则；
②若，则一元二次方程有两个不相等的实数根；
③若，则一元二次方程有两个不相等的实数根；
④若，则二次函数的图像与坐标轴的公共点的个数是2或3.
其中正确的是（　　）．

A．只有①②③

B．只有①③④

C．只有①④

D．只有②③④．

若二次函数y=x²-6x+c的图像过A（-1，y₁）、B（2，y₂）、C（5，y₃）三点，则y_1、y_2、y₃大小关系正确的是（   ）

A．y1>y2>y3

B．y1>y3 >y2

C．y2>y1>y3

D．y3>y1>y2

若二次函数y=ax²+bx+c（a＜0）的图象如图所示，且关于x的方程ax²+bx+c=k有两个不相等的实根，则常数k的取值范围是（    ）

A．0＜k＜4

B．-3＜k＜1

C．k＜-3或k＞1

D．k＜4

抛物线y=﹣x²+bx+c的部分图象如图所示，要使y＞0，则x的取值范围是（ ）

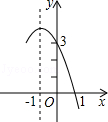
A．﹣4＜x＜1

B．﹣3＜x＜1

C．x＜﹣4或x＞1

D．x＜﹣3或x＞1

抛物线y=3x²向左平移1个单位，再向上平移2个单位，所得到的抛物线是（ ）

A．y=3（x﹣1）^2﹣2

B．y=3（x+1）^2﹣2

C．y=3（x+1）^2+2

D．y=3（x﹣1）^2+2

如图，抛物线y=ax²+bx+c（a＞0）的对称轴是直线x=1，且经过点P（3，0），则a﹣b+c的值为（   ）

A．0

B．﹣1

C．1

D．2

对于二次函数的图象，下列说法正确的是（ ）

A．开口向上

B．对称轴是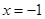

C．顶点坐标是（1，2）

D．与x轴有两个交点

把抛物线向左平移3个单位，再向上平移2个单位所得抛物线的解析式为（    ）

A．	B．
C．	D．

已知点（-1，y₁），（-2，y₂），（2，y₃）在函数y=2（x-1）²的图象上，则y₁、y₂、y₃的大小关系是（  ）

A．y1＞y2＞y3

B．y2＞y1＞y3

C．y2＞y3＞y1

D．y3＞y1＞y2

在二次函数y=ax²+bx+c，x与y的部分对应值如下表：

x	…	-2	0	2	3	…
y	…	8	0	0	3	…

则下列说法：
①图象经过原点；
②图象开口向下；
③图象经过点（-1，3）；
④当x＞0时，y随x的增大而增大；
⑤方程ax²+bx+c=0有两个不相等的实数根．
其中正确的是（）
A、①②③        B、①③⑤         C、①③④           D、①④⑤

当时，与的图象大致是（  ）

如下右图，A点在半径为2的⊙O上，过线段OA上的一点P作直线l，与过A点的切线交于点B，且∠APB=60°．设OP=x，则△PAB的面积y关于x的函数图象大致是

如图，抛物线y₁=a(x＋2)²－3与交于点A(1，3)，过点A作x轴的平行线，分别交两条抛物线于点B、C，则以下结论：①无论x取何值，y₂总是正数；②a=1；③当x=0时，y₂－y₁=4；④2AB=3AC．其中正确的是（    ）

A．①②             B．②③           C．③④         D．①④