已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.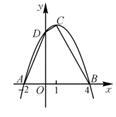
(1)求二次函数的解析式;
(2)设此二次函数图象的顶点为C,与y轴交点为D,求四边形ABCD的面积.
已知抛物线y=-2x2+12x-13,则下列关于此抛物线说法正确的是( )
| A.开口向下,对称轴为直线x=-3 |
| B.顶点坐标为(-3,5) |
| C.最小值为5 |
| D.当x>3时,y随x的增大而减小 |
已知某二次函数的图象如图所示,则这个二次函数的解析式为( )

| A.y=-3(x-1)2+3 | B.y=3(x-1)2+3 |
| C.y=-3(x+1)2+3 | D.y=3(x+1)2+3 |
如果将二次函数y=3x2的图象向上平移5个单位,得到新的图象的二次函数表达式是( )
| A.y=3x2-5 | B.y=3(x-5)2 | C.y=3x2+5 | D.y=3(x+5)2-5 |
已知二次函数y= (x﹣h)2+4,当x>﹣1时,y随x的增大而增大,则有( )
(x﹣h)2+4,当x>﹣1时,y随x的增大而增大,则有( )
| A.h≥﹣1 | B.h>﹣1 | C.h<﹣1 | D.h≤﹣1 |
已知点(﹣2,5),(4,5)是抛物线上的两点,则此抛物线的对称轴为( )
| A.x=﹣2 | B.x="2" | C.x="1" | D.无法确定 |
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c=-9a;④若(-3,y1),( ,y2)是抛物线上两点,则y1>y2,其中正确的个数是( )
,y2)是抛物线上两点,则y1>y2,其中正确的个数是( )

| A.1个 | B.2个 | C.3个 | D.4个 |
如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,OC=4,抛物线y=x2+bx+c经过A,B两点,抛物线的顶点为D.
(1)求b,c的值;
(2)点E是直角三角形ABC斜边AB上一动点(点A、B除外),过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
(3)在(2)的条件下:
①求以点E、B、F、D为顶点的四边形的面积;
②在抛物线上是否存在一点P,使△EFP是以EF为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,说明理由.
关于二次函数y=ax2+bx+c的图象有下列命题:
①当c=0时,函数的图象经过原点;
②当c>0,且函数的图象开口向下时,方程ax2+bx+c=0必有两个不相等的实根;
③函数图象最高点的纵坐标是 ;
;
④当b=0时,函数的图象关于y轴对称.
其中正确命题的个数是( )
| A.1个 | B.2个 | C.3个 | D.4个 |