定义:f(a,b)=(b,a),g(m,n)=(﹣m,﹣n).例如f(2,3)=(3,2),g(﹣1,﹣4)=(1,4).则g[f(﹣5,6)]等于【 】
| A.(﹣6,5) | B.(﹣5,﹣6) | C.(6,﹣5) | D.(﹣5,6) |
小亮的父亲想购买同一种大小一样、形状相同的地板砖铺设地面,小亮根据所学知识告诉父亲,为了能够做到无缝隙、不重叠地铺设,购买的地板砖形状不能是( )
| A.正三角形 | B.正方形 | C.正五边形 | D.正六边形 |
下列图形都是由同样大小的平行四边形按一定的规律组成,其中,第①个图形中一共有1个平行四边形,第②个图形中一共有5个平行四边形,第③个图形中一共有11个平行四边形,…则第⑥个图形中平行四边形的个数为( )
| A.55 | B.42 | C.41 | D.29 |
对点(x,y )的一次操作变换记为P 1(x,y ),定义其变换法则
如下:P 1(x,y )=(  ,
,  );且规定
);且规定  (
(  为大于1的整数).如
为大于1的整数).如
P 1(1,2 )=(3,  ),P 2(1,2 )= P 1(P 1(1,2 ))= P 1(3,
),P 2(1,2 )= P 1(P 1(1,2 ))= P 1(3,  )=(2,4),P 3(1,
)=(2,4),P 3(1,
2 )= P 1(P 2(1,2 ))= P 1(2,4)=(6,  ).则P 2011(1,
).则P 2011(1,  )=( )
)=( )
| A. | (0,2 1005) | B. | (0,-2 1005) | C. | (0,-2 1006) | D. | (0,2 1006) |
将一张长与宽的比为2∶1的长方形纸片按如图①、②所示的方式对折,然后沿图③中的虚线裁剪,得到图④,最后将图④的纸片再展开铺平,则所得到的图案是( )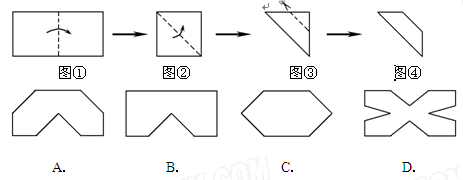
用边长相等的黑色正三角形与白色正六边形镶嵌图案,按图①②③所示的规律依次下去,则第 个图案中,所包含的黑色正三角形和白色正六边形的个数总和是( )
个图案中,所包含的黑色正三角形和白色正六边形的个数总和是( )
A. |
B.6n+1 | C. |
D. |
下列说法正确的是 ( ▲ )
| A.要了解一批灯泡的使用寿命,采用全面调查的方式 |
| B.要了解全市居民对环境的保护意识,采用抽样调查的方式 |
| C.一个游戏的中奖率是1%,则做100次这这样的游戏一定会中奖 |
D.若甲组数据的方差 ,乙组数据的方差 ,乙组数据的方差 ,则乙组数据比甲组数据稳定 ,则乙组数据比甲组数据稳定 |
如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2010次输出的结果为 ( )
| A.6 | B.3 | C. | D.+3×1003 |
一个几何体的三视图如图所示,网格中小正方形的边长均为1,那么下列选项中最接近这个几何体的侧面积的是( )
| A.24.0 | B.62.8 | C.74.2 | D.113.0 |

.商场将某种商品按标价的八折出售,仍可获利90元,若这种商品的标价为300元,则该商品的进价为 ( ).
| A.330元 | B.210元 | C.180元 | D.150元 |
将一张正方形纸片如图所示折叠两次,并在上面剪下一个菱形小洞,纸片展开后( )
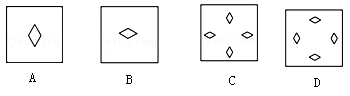
有20个同学排成一行,若从左往右隔1人报数,小李报8号;若从右往左隔2人报数,小陈报6号.那么,从小陈开始向小李逐人报数,小李报的号数为( ).
| A.ll | B.12 | C.13 | D.14 |
右边的图案是由下面五种基本图形中的两种拼接而成,这两种基本图形是
| A.②⑤ | B.②④ | C.③⑤ | D.①⑤ |
.天安门广场的面积约为44万平方千米,请你估算以下,它的百万分之一大约相当于
| A.一教室地面的面积 | B.黑板面面积 |
| C.课桌面的面积 | D.铅笔盒盒面的面积 |