初中数学折线统计图试题

小明为了了解气温对用电量的影响，对去年自己家的每月用电量和当地气温进行了统计．当地去年每月的平均气温如图1，小明家去年月用电量如图2．

根据统计图，回答下面的问题：

（1）当地去年月平均气温的最高值、最低值各为多少？相应月份的用电量各是多少？

（2）请简单描述月用电量与气温之间的关系；

（3）假设去年小明家用电量是所在社区家庭年用电量的中位数，据此他能否预测今年该社区的年用电量？请简要说明理由．

为积极创建全国文明城市，某市对某路口的行人交通违章情况进行了20天的调查，将所得数据绘制成如下统计图（图2不完整） $:$

请根据所给信息，解答下列问题：

（1）第7天，这一路口的行人交通违章次数是多少次？这20天中，行人交通违章6次的有多少天？

（2）请把图2中的频数直方图补充完整；（温馨提示：请画在答题卷相对应的图上）

（3）通过宣传教育后，行人的交通违章次数明显减少．经对这一路口的再次调查发现，平均每天的行人交通违章次数比第一次调查时减少了4次，求通过宣传教育后，这一路口平均每天还出现多少次行人的交通违章？

为监测某河道水质，进行了6次水质检测，绘制了如图的氨氮含量的折线统计图．若这6次水质检测氨氮含量平均数为 $1.5\mathit{mg}/L$，则第3次检测得到的氨氮含量是　　 $\mathit{mg}/L$．

某汽车厂去年每个季度汽车销售数量（辆 $)$占当季汽车产量（辆 $)$百分比的统计图如图所示．根据统计图回答下列问题：

（1）若第一季度的汽车销售量为2100辆，求该季的汽车产量；

（2）圆圆同学说：“因为第二，第三这两个季度汽车销售数量占当季汽车产量是从 $75\%$降到 $50\%$，所以第二季度的汽车产量一定高于第三季度的汽车产量”，你觉得圆圆说的对吗？为什么？

绵阳某公司销售部统计了每个销售员在某月的销售额， 绘制了如下折线统计图和扇形统计图：

设销售员的月销售额为 $x$（单 位： 万元） ． 销售部规定： 当 $x<16$时为“不称职”， 当 $16⩽x<20$时为“基本称职”， 当 $20⩽x<25$时为“称职”， 当 $x⩾25$时为“优秀” ． 根据以上信息， 解答下列问题：

（1） 补全折线统计图和扇形统计图；

（2） 求所有“称职”和“优秀”的销售员月销售额的中位数和众数；

（3） 为了调动销售员的积极性， 销售部决定制定一个月销售额奖励标准， 凡月销售额达到或超过这个标准的销售员将获得奖励 ． 如果要使得所有“称职”和“优秀”的销售员的一半人员能获奖， 月销售额奖励标准应定为多少万元 （结 果取整数） ？并简述其理由 ．

西昌市教科知局从2013年起每年对全市所有中学生进行“我最喜欢的阳光大课间活动”抽样调查（被调查学生每人只能选一项），并将抽样调查的数据绘制成图1、图2两幅统计图，根据统计图提供的信息解答下列问题：

（1）　　年抽取的调查人数最少；　　年抽取的调查人数中男生、女生人数相等；

（2）求图2中“短跑”在扇形图中所占的圆心角 $\alpha$的度数；

（3）2017年抽取的学生中，喜欢羽毛球和短跑的学生共有多少人？

（4）如果2017年全市共有3.4万名中学生，请你估计我市2017年喜欢乒乓球和羽毛球两项运动的大约有多少人？

如图是成都市某周内日最高气温的折线统计图，关于这7天的日最高气温的说法正确的是 $($　　 $)$

A．极差是 $8^{°}\text{C}$B．众数是 ${28}^{°}\text{C}$C．中位数是 ${24}^{°}\text{C}$D．平均数是 ${26}^{°}\text{C}$

为积极响应“弘扬传统文化”的号召，某学校倡导全校1200名学生进行经典诗词诵背活动，并在活动之后举办经典诗词大赛，为了解本次系列活动的持续效果，学校团委在活动启动之初，随机抽取部分学生调查“一周诗词诵背数量”，根据调查结果绘制成的统计图（部分）如图所示．

大赛结束后一个月，再次抽查这部分学生“一周诗词诵背数量”，绘制成统计表

一周诗词诵背数量	3首	4首	5首	6首	7首	8首
人数	10	10	15	40	25	20

请根据调查的信息分析：

（1）活动启动之初学生“一周诗词诵背数量”的中位数为　　；

（2）估计大赛后一个月该校学生一周诗词诵背6首（含6首）以上的人数；

（3）选择适当的统计量，从两个不同的角度分析两次调查的相关数据，评价该校经典诗词诵背系列活动的效果．

近几年，随着电子商务的快速发展，“电商包裹件”占“快递件”总量的比例逐年增长，根据企业财报，某网站得到如下统计表：

年份	2014	2015	2016	2017（预计）
快递件总量（亿件）	140	207	310	450
电商包裹件（亿件）	98	153	235	351

（1）请选择适当的统计图，描述 $2014-2017$年“电商包裹件”占当年“快递件”总量的百分比（精确到 $1\%$）；

（2）若2018年“快递件”总量将达到675亿件，请估计其中“电商包裹件”约为多少亿件？

自新冠肺炎疫情爆发以来，我国人民上下一心，团结一致，基本控制住了疫情．然而，全球新冠肺炎疫情依然严重，境外许多国家的疫情尚在继续蔓延，疫情防控不可松懈．如图是某国截止5月31日新冠病毒感染人数的扇形统计图和折线统计图．

根据上面图表信息，回答下列问题：

（1）截止5月31日该国新冠肺炎感染总人数累计为　　万人，扇形统计图中 $40-59$岁感染人数对应圆心角的度数为　　 $°$；

（2）请直接在图中补充完整该国新冠肺炎感染人数的折线统计图；

（3）在该国所有新冠肺炎感染病例中随机地抽取1人，求该患者年龄为60岁或60岁以上的概率；

（4）若该国感染病例中从低到高各年龄段的死亡率依次为 $1\%$、 $2.75\%$、 $3.5\%$、 $10\%$、 $20\%$，求该国新冠肺炎感染病例的平均死亡率．

甲、乙两人连续5次射击成绩如图所示，下列说法中正确的是 $($　　 $)$

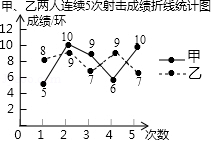
A．甲的成绩更稳定B．乙的成绩更稳定

C．甲、乙的成绩一样稳定D．无法判断谁的成绩更稳定

小明在体考时选择了投掷实心球，如图是体育老师记录的小明在训练时投掷实心球的6次成绩的折线统计图．这6次成绩的中位数是　　．

某企业 $1-6$月份利润的变化情况如图所示，以下说法与图中反映的信息相符的是 $($　　 $)$

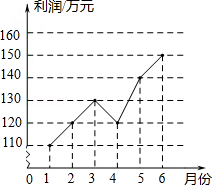
A． $1-6$月份利润的众数是130万元

B． $1-6$月份利润的中位数是130万元

C． $1-6$月份利润的平均数是130万元

D． $1-6$月份利润的极差是40万元

某校举办“打造平安校园”活动，随机抽取了部分学生进行校园安全知识测试．将这些学生的测试结果分为四个等级： $A$级：优秀； $B$级：良好； $C$级：及格； $D$级：不及格，并将测试结果绘制成如下统计图．请你根据图中信息，解答下列问题：

（1）本次参加校园安全知识测试的学生有多少人？

（2）计算 $B$级所在扇形圆心角的度数，并补全折线统计图；

（3）若该校有学生1000名，请根据测试结果，估计该校达到及格和及格以上的学生共有多少人？

某球员参加一场篮球比赛，比赛分4节进行，该球员每节得分如折线统计图所示，则该球员平均每节得分为 $($　　 $)$

A．7分B．8分C．9分D．10分