如图,双曲线y= 与矩形OABC的对角线OB相交于点D,且DB:OD=2:3,则矩形OABC的面积为()
与矩形OABC的对角线OB相交于点D,且DB:OD=2:3,则矩形OABC的面积为()
A. |
B. |
C. |
D.8 |
如图,正比例函数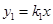 的图象与反比例函数
的图象与反比例函数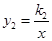 的图象相交于A,B两点,其中点A的横坐标为2,当
的图象相交于A,B两点,其中点A的横坐标为2,当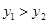 时,x的取值范围是()
时,x的取值范围是()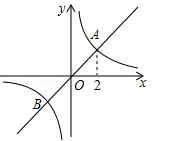
| A.x<﹣2或x>2 |
| B.x<﹣2或0<x<2 |
| C.﹣2<x<0或0<x<﹣2 |
| D.﹣2<x<0或x>2 |
如果反比例函数 的图像经过点(-3,-4),那么函数的图象应在()
的图像经过点(-3,-4),那么函数的图象应在()
| A.第一、三象限 | B.第一、二象限 |
| C.第二、四象限 | D.第三、四象限 |
当x>0时,函数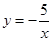 的图象在()
的图象在()
| A.第四象限 | B.第三象限 | C.第二象限 | D.第一象限 |
如图,直线 和双曲线y=
和双曲线y= (
( )交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为
)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为 、△BOD的面积为
、△BOD的面积为 、△POE的面积为
、△POE的面积为 ,则()
,则()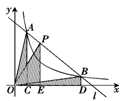
A.S1<s2<s3B.S1>s2>s3
C.S1=s2<s3D.S1=s2>s3
已知函数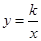 的图象过点
的图象过点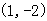 ,则该函数的图象必在()
,则该函数的图象必在()
| A.第二、三象限 | B.第二、四象限 |
| C.第一、三象限 | D.第三、四象限 |
面积为2的△ABC,一边长为x,这边上的高为y,则y与x的变化规律用图象表示大致是()
A.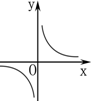 |
B. |
C. |
D. |
正比例函数y=2x与反比例函数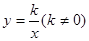 的图象有一个交点为(2,4),则另一个交点坐标为()
的图象有一个交点为(2,4),则另一个交点坐标为()
A.(2,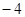 ) ) |
B.(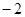 , ,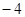 ) ) |
C.(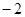 ,4) ,4) |
D.(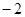 , ,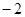 ) ) |
下列各点中,在反比例函数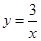 图象上的是()
图象上的是()
A.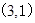 |
B. |
C.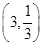 |
D.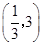 |
如图,过双曲线y= (k是常数,k>0,x>0)的图象上两点A,B分别作AC⊥x轴于C,BD⊥x轴于D,则△AOC的面积S1和△BOD的面积S2的大小关系为()
(k是常数,k>0,x>0)的图象上两点A,B分别作AC⊥x轴于C,BD⊥x轴于D,则△AOC的面积S1和△BOD的面积S2的大小关系为()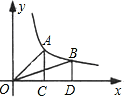
| A.S1>S2 | B.S1=S2 |
| C.S1<S2 | D.S1与S2无法确定 |