已知菱形的两条对角线长分别是6和8,则这个菱形的面积为 .
如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若AC=4,则四边形CODE的周长是 .
如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE,EF⊥AB,垂足为F,连接DF,当 =时,四边形ADFE是平行四边形.
=时,四边形ADFE是平行四边形.
如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为.
如图,
,
,
,在
中截出一个正方形
,使点
,
分别在
,
边上,边
在
边上;在
在截出第二个正方形
,使点
,
分别在
,
边上,边
在
边上;…,依此方法作下去,则第
个正方形的边长为.
如图,在平面直角坐标系中,矩形OABC,OA=3,OC=6,将△ABC沿对角线AC翻折,使点B落在点B′处,AB′与y轴交于点D,则点D的坐标为.
如图,M、N分别是正方形ABCD边DC、AB的中点,分别以AE、BF为折痕,使点D、点C落在MN的点G处,则△ABG是三角形.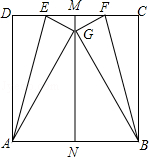
如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为.
如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件(只添一个即可),使四边形ABCD是平行四边形.
如图,将矩形ABCD沿对角线BD折叠,使点C与C′重合.若AB=3,则C′D的长为.
如图,在四边形ABCD中,已知AB∥DC,AB=DC.在不添加任何辅助线的前提下,要想该四边形成为矩形,只需再加上的一个条件是.(填上你认为正确的一个答案即可)