初中数学圆内接四边形的性质试题

如图所示，在菱形ABCD中，AB=4，∠BAD=120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．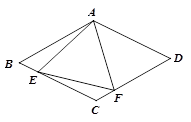

（1）证明不论E、F在BC．CD上如何滑动，总有BE=CF；
（2）当点E、F在BC．CD上滑动时，分别探讨四边形AECF的面积和△CEF的周长是否发生变化？如果不变，求出这个定值；如果变化，求出最小值．

已知菱形的周长为，一条对角线长为，则这个菱形的面积为           （）．

如图，沿AE折叠矩形纸片ABCD，使点D落在BC边的点F处．已知AB=8，BC=10，则tan∠EFC的值为 （   ）

A．

B．

C．

D．

五边形的内角和为________度，十二边形的外角和为_________度．

如图，四边形ABCD、DEFG都是正方形，连接AE、CG、AE与CG相交于点M，CG与AD相交于点N．

求证：（1）；
（2）

我们把两条中线互相垂直的三角形称为“中垂三角形”．例如图1，图2，图3中，AF，BE是△ABC的中线， AF⊥BE ， 垂足为P．像△ABC这样的三角形均为“中垂三角形”．设，，．
特例探索
（1）如图1，当∠=45°，时，=             ，              ；
如图2，当∠=30°，时，  =             ，              ；

归纳证明
（2）请你观察（1）中的计算结果，猜想三者之间的关系，用等式表示出来，并利用图3证明你发现的关系式；
拓展应用
（3）如图4，在□ABCD中，点E，F，G分别是AD，BC，CD的中点，BE⊥EG， AD= ，AB=3．求AF的长．

如图，在矩形ABCD中，对角线与相交于点O，且AB=OA=2cm ，则BD的长为________cm，BC的长为_______cm．

顺次连结对角线相等的四边形各边中点所得到的四边形一定是（    ）

A．平行四边形

B．矩形

C．菱形

D．正方形

如图，正方形ABCB₁中，AB=1．AB与直线l的夹角为30°，延长CB₁交直线l于点A₁，作正方形A₁B₁C₁B₂，延长C₁B₂交直线l于点A₂，作正方形A₂B₂C₂B₃，延长C₂B₃交直线l于点A₃，作正方形A₃B₃C₃B₄，…，依此规律，则A₂₀₁₄A₂₀₁₅=            ．

如果一个正多边形的中心角为45°，那么这个正多边形的边数是           ．

用形状、大小完全相等的下列图形不能进行密铺的是（ ）

A．等腰三角形	B．平行四边形
C．正五边形	D．正六边形

正多边形的每个外角都为60°，它是           边形．

如图的平行四边形ABCD中，线段CD是由AB      而得，而△AOD可以看作是由△COB      而来的．

菱形的两条对角线长分别为6和8，则菱形的面积是（ ）

A．10

B．20

C．24

D．48

如图，将长方形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在对角线D′处．若AB=3，AD=4，则ED的长为（ ）

A．

B．2

C．1

D．