如图, 的半径为6, 是 的内接三角形,连接 、 ,若 与 互补,则线段 的长为

A. B.3C. D.6
如图, , 分别是 的直径和弦, 于点 ,连接 , ,且 , ,则 的长为

| A. |
|
B. |
4 |
C. |
|
D. |
4.8 |
如图,在平面直角坐标系中, 与 轴相切于点 ,与 轴分别交于点 和点 ,则圆心 到坐标原点 的距离是
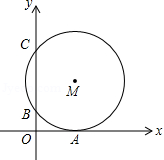
A.10B. C. D.
下列说法正确的是
| A. |
.垂直于直径的弦平分这条直径 |
| B. |
.负数没有立方根 |
| C. |
.两条对角线互相垂直的四边形是菱形 |
| D. |
.三角形两边的差小于第三边 |
如图, 是 的直径,弦 ,垂足为点 ,连接 , .如果 , ,那么图中阴影部分的面积是

A. B. C. D.
如图,在 中,弦 垂直平分半径 ,垂足为 ,若点 是 上异于点 、 的任意一点,则
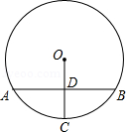
| A. |
或 |
B. |
或 |
C. |
或 |
D. |
或 |
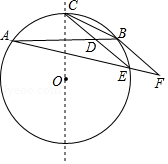
如图所示 为 的一条弦,点 为劣弧 的中点, 为优弧 上一点,点 在 的延长线上,且 ,线段 交弦 于点 .
①求证: ;
②若 ,且 ,求 的面积(注:根据圆的对称性可知 .
(年贵州省黔南州)如图,AB是⊙O的直径,CD为弦,CD⊥AB且相交于点E,则下列结论中不成立的是( )
| A.∠A=∠D | B. |
C.∠ACB="90°" | D.∠COB=3∠D |
如图, 是 的直径,弦 于点 ,连结 , .若 的半径为 , ,则下列结论一定成立的是
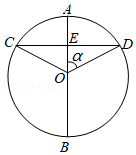
| A. |
|
B. |
|
| C. |
|
D. |
|
学习圆的性质后,小铭与小熹就讨论起来,小铭说:"被直径平分的弦也与直径垂直",小熹说:"用反例就能说明这是假命题".下列判断正确的是
| A. |
两人说的都对 |
| B. |
小铭说的对,小熹说的反例不存在 |
| C. |
两人说的都不对 |
| D. |
小铭说的不对,小熹说的反例存在 |
如图, 中,半径 弦 于点 ,点 在 上, , ,则半径 等于
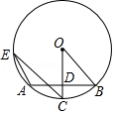
A. B.2C. D.3
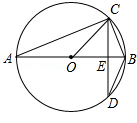
如图,四边形 为 的内接四边形.延长 与 相交于点 , ,垂足为 ,连接 , ,则 的度数为

A. B. C. D.