初中数学矩形的判定与性质试题

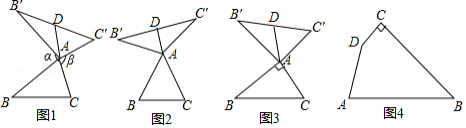
我们定义：如图1，在中，把绕点顺时针旋转得到，把绕点逆时针旋转得到，连接．当时，我们称△是的“旋补三角形”，△ 边上的中线叫做的“旋补中线”，点叫做“旋补中心”．

特例感知：

（1）在图2，图3中，△是的“旋补三角形”， 是的“旋补中线”．

①如图2，当为等边三角形时，与的数量关系为　　；

②如图3，当，时，则长为　　．

猜想论证：

（2）在图1中，当为任意三角形时，猜想与的数量关系，并给予证明．

拓展应用

（3）如图4，在四边形，，，，，．在四边形内部是否存在点，使是的“旋补三角形”？若存在，给予证明，并求的“旋补中线”长；若不存在，说明理由．