初中数学勾股定理的证明试题

（1）阅读理解

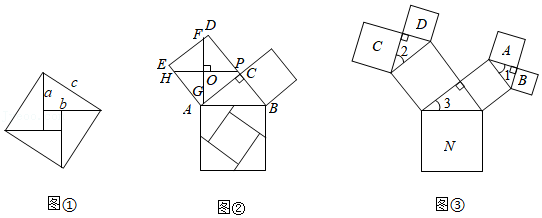
我国是最早了解勾股定理的国家之一，它被记载于我国古代的数学著作《周髀算经》中．汉代数学家赵爽为了证明勾股定理，创制了一幅如图①所示的“弦图”，后人称之为“赵爽弦图”．

根据“赵爽弦图”写出勾股定理和推理过程；

（2）问题解决

勾股定理的证明方法有很多，如图②是古代的一种证明方法：过正方形 $\mathit{ACDE}$的中心 $O$，作 $\mathit{FG}\perp \mathit{HP}$，将它分成4份，所分成的四部分和以 $\mathit{BC}$为边的正方形恰好能拼成以 $\mathit{AB}$为边的正方形．若 $\mathit{AC}=12$， $\mathit{BC}=5$，求 $\mathit{EF}$的值；

（3）拓展探究

如图③，以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程就可以得到“勾股树”的部分图形．设大正方形 $N$的边长为定值 $n$，小正方形 $A$， $B$， $C$， $D$的边长分别为 $a$， $b$， $c$， $d$．

已知 $\angle 1=\angle 2=\angle 3=\alpha$，当角 $\alpha (0°<\alpha <90°)$变化时，探究 $b$与 $c$的关系式，并写出该关系式及解答过程 $(b$与 $c$的关系式用含 $n$的式子表示）．