阅读下面材料:
小明遇到这样一个问题:
如图1, 中, ,点 在 上,且 ,求证: .
小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:
方法1:如图2,作 平分 ,与 相交于点 .
方法2:如图3,作 ,与 相交于点 .
(1)根据阅读材料,任选一种方法,证明 .
用学过的知识或参考小明的方法,解决下面的问题:
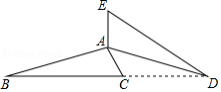
(2)如图4, 中,点 在 上,点 在 上,且 ,点 在 上,且 ,延长 、 ,相交于点 ,且 .
①在图中找出与 相等的角,并加以证明;
②若 ,猜想线段 与 的数量关系,并证明你的猜想.

如图,将 绕点 逆时针旋转 ,得到 ,这时点 , , 恰好在同一直线上,则 的度数为 .
如图所示,在等腰 中, , ,将 中的 沿 向下翻折,使点 落在点 处.若 ,则 的长是 .

一个三角形的三个内角的度数之比为 ,则这个三角形一定是
A.锐角三角形B.直角三角形
C.钝角三角形D.等腰直角三角形
如图,直线 ,直线 与 、 分别相交于 、 两点,过点 作直线 的垂线交直线 于点 ,若 ,则 的度数为

A. B. C. D.
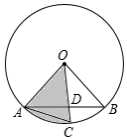
如图,已知半径为1的 上有三点 、 、 , 与 交于点 , , ,则阴影部分的扇形 面积是 .
如图, 是以 为斜边的等腰直角三角形, 中, , , 中点为 , 与 的延长线交于点 ,则 的度数为

A. B. C. D.