初中数学多项式乘多项式选择题

我国古代数学的许多创新和发展都位居世界前列，如南宋数学家杨辉（约13世纪）所著的《详解九章算术》一书中，用如图的三角形解释二项式 ${(a+b)}^n$的展开式的各项系数，此三角形称为“杨辉三角”．

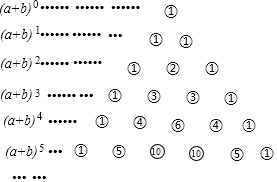
根据“杨辉三角”请计算 ${(a+b)}^{20}$的展开式中第三项的系数为 $($　　 $)$

A．2017B．2016C．191D．190

下列计算结果正确的是（　　）

A．	3+ $\mathrm{}\sqrt{3}$ ＝3 $\mathrm{}\sqrt{3}$
B．	（m﹣n）（m ^2+mn+n ^2）＝m ^3﹣n ^3
C．	（﹣2b ^2） ^3＝﹣6b ^6
D．	（﹣a） ^2•a ^6＝﹣a ^8

下列计算正确的是 $($　　 $)$

A． $a^2·a^3=a^6$B． $(a+b)(a-2b)=a^2-2b^2$

C． ${\left(a{b}^3\right)}^2=a^2{b}^6$D． $5a-2a=3$

下列运算正确的是 $($　　 $)$

A． $a^2·a^5=a^{10}$B． ${\left(3a^3\right)}^2=6a^6$

C． ${(a+b)}^2=a^2+b^2$D． $(a+2)(a-3)=a^2-a-6$

下列运算正确的是（　　）

A．	﹣2x ^2y•3xy ^2＝﹣6x ^2y ^2	B．	（﹣x﹣2y）（x+2y）＝x ^2﹣4y ^2
C．	6x ^3y ^2÷2x ^2y＝3xy	D．	（4x ^3y ^2） ^2＝16x ^9y ^4

计算 $(x+1)(x+2)$的结果为 $($　　 $)$

A． $x^2+2$B． $x^2+3x+2$C． $x^2+3x+3$D． $x^2+2x+2$

下列运算中，计算正确的是 $($　　 $)$

A． ${\left(a^{2}b\right)}^3=a^5{b}^3$B． ${\left(3a^2\right)}^3=27a^6$C． $x^6÷x^2=x^3$D． ${(a+b)}^2=a^2+b^2$

下列计算正确的是 $($　　 $)$

A． $(a+2)(a-2)=a^2-2$B． $(a+1)(a-2)=a^2+a-2$

C． ${(a+b)}^2=a^2+b^2$D． ${(a-b)}^2=a^2-2\mathit{ab}+b^2$

正整数 x、 y满足（2 x﹣5）（2 y﹣5）＝25，则 x+ y等于（　　）

A．

18或10

B．

18

C．

10

D．

26

下列运算正确的是 $($　　 $)$

A． $a^2+2a=3a^3$B． ${(-2a^3)}^2=4a^5$

C． $(a+2)(a-1)=a^2+a-2$D． ${(a+b)}^2=a^2+b^2$

下列运算正确的是 $($ 　　 $)$

A．	$(a+b)(a-2b)=a^2-2b^2$	B．	${(a-\frac{1}{2})}^2=a^2-\frac{1}{4}$
C．	$-2(3a-1)=-6a+1$	D．	$(a+3)(a-3)=a^2-9$

计算 $(a-2)(a+3)$的结果是 $($　　 $)$

A． $a^2-6$B． $a^2+a-6$C． $a^2+6$D． $a^2-a+6$

计算（2x﹣1）（1﹣2x）结果正确的是（　　）

A．4x²﹣1B．1﹣4x²C．﹣4x²+4x﹣1D．4x²﹣4x+1

我国南宋数学家杨辉所著的《详解九章算术》一书中，用如图的三角形解释二项式 ${(a+b)}^n$的展开式的各项系数，此三角形称为“杨辉三角”

根据”杨辉三角”请计算 ${(a+b)}^8$的展开式中从左起第四项的系数为 $($　　 $)$

A．84B．56C．35D．28

下列计算正确的是 $($ 　　 $)$

A．	$2x+3y=5\mathit{xy}$	B．	$(x+1)(x-2)=x^2-x-2$
C．	$a^2·a^3=a^6$	D．	${(a-2)}^2=a^2-4$