有一个十进制的六位数 (其中a、b、c、d、e分别是这个六位数的万位、千位、百位、十位、个位上的数字)乘以3后,变成一个新的六位数
(其中a、b、c、d、e分别是这个六位数的万位、千位、百位、十位、个位上的数字)乘以3后,变成一个新的六位数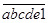 ,则原来的六位数
,则原来的六位数 是.
是.
观察下面由正整数组成的数阵:
照此规律,按从上到下、从左到右的顺序,第50行的第50个数是()
| A.2450 | B.2451 | C.2550 | D.2551 |
如图是由等圆组成的一组图,第①个图由1个圆组成,第②个图由5个圆组成,第③个图由12个圆组成…按此规律排列下去,则第⑥个图由个圆组成.
如图是一个点阵,从上往下有无数多行,其中第一行有2个点,第二行有5个点,第三行有11个点,第四行有23个点,…,按此规律,第n行有个点.
a是不为1的数,我们把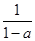 称为a的差倒数,如:2的差倒数为
称为a的差倒数,如:2的差倒数为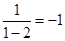 ;
;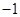 的差倒数是
的差倒数是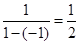 ;已知
;已知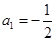 ,
,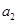 是
是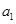 的差倒数,
的差倒数,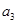 是
是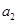 的差倒数.
的差倒数.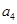 是
是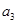 差倒数,…依此类推,则
差倒数,…依此类推,则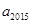 =.
=.
在求1+6+62+63+64+65+66+67+68+69的值时,小林发现:从第二个加数起每一个加数都是前一个加数的6倍,于是她设:
S=1+6+62+63+64+65+66+67+68+69①
然后在①式的两边都乘以6,得:
6S=6+62+63+64+65+66+67+68+69+610②②-①得6S-S=610-1,即5S=610-1,所以S=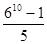 ,得出答案后,爱动脑筋的小林想:如果把“6”换成字母“a”(a≠0且a≠1),能否求出1+a+a2+a3+a4+…+a2015的值?你的答案是.
,得出答案后,爱动脑筋的小林想:如果把“6”换成字母“a”(a≠0且a≠1),能否求出1+a+a2+a3+a4+…+a2015的值?你的答案是.
如图,是一组按照某种规律摆放而成的图案,第1个图有1个三角形,第二个图有4个三角形,第三个图有8个三角形,第四个图有12个三角形,则图5中三角形的个数是()
| A.8 | B.12 | C.16 | D.17 |
对点(x,y)的一次操作变换记为P1(x,y),定义其变换法则如下:P1(x,y)=(x+y,x﹣y);且规定Pn(x,y)=P1(Pn﹣1(x,y))(n为大于1的整数).如P1(1,2)=(3,﹣1),P2(1,2)=P1(P1(1,2))=P1(3,﹣1)=(2,4),P3(1,2)=P1(P2(1,2))=P1(2,4)=(6,﹣2).则P2015(1,﹣1)=______________.
若x是不等于1的实数,我们把 称为x的差倒数,如2的差倒数是
称为x的差倒数,如2的差倒数是 ,-1的差倒数为
,-1的差倒数为 ,现已知,x1=
,现已知,x1= ,x2是x1的差倒数, x3是x2的差倒数,x4是x3的差倒数,……,依次类推,则x2015=.
,x2是x1的差倒数, x3是x2的差倒数,x4是x3的差倒数,……,依次类推,则x2015=.
记 ,令
,令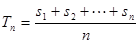 ,则称
,则称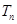 为
为 ,
, ,……,
,……, 这列数的“凯森和”.已知
这列数的“凯森和”.已知 ,
, ,……,
,……,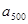 的“凯森和”为2004,那么13,
的“凯森和”为2004,那么13, ,
, ,……,
,……,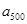 的“凯森和”为()
的“凯森和”为()
| A.2013 | B.2015 | C.2017 | D.2019 |
定义一种运算: ,其中k是正整数,且k ≥2,[x]表示非
,其中k是正整数,且k ≥2,[x]表示非
负实数x的整数部分,例如[2.6]=2,[0.8]=0.若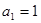 ,则
,则 的值为()
的值为()
| A.2015 | B.4 | C.2014 | D.5 |