小学数学格点面积（毕克定理）解答题

有两个水池，甲水池长8米，宽6米，水深3米，乙水池空着，它长、宽高都是4米．现将从甲水池中抽出一部分水到乙水池，使两水池的水面同样高．求水面的高度．

一条直线上放着一个长和宽分别为4厘米和3厘米的长方形I（如图）．让这个长方形绕顶点B顺时针旋转90°后到达长方形Ⅱ的位置，这样连续做三次，A点到达E点的位置．求A点经过的总路程的长度．（圆周率按3计算）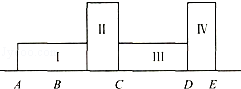

用一块面积为36平方厘米的圆形铝板下料，如图所示：裁出七个同样大小的圆铝板．问：所余下的边角料的总面积是多少平方厘米？

有一个长方体水池，底面为边长60厘米的正方形，里面插着一根长1米的木桩，木桩的底面是一个边长15厘米的正方形，木桩有一部分浸在水中，一部分露出水面．现在将木桩提起来24厘米（仍有部分浸在水里），那么露出水面的木桩浸湿部分面积为多少平方厘米？

如图一个底面长30分米，宽10分米，高12分米的长方体水池，存有四分之三池水，请问：
（1）将一个高11分米，体积330立方分米的圆柱放入池中，水面的高度变为多少分米？
（2）如果再放入一个同样的圆柱，水面高度又变成了多少分米？
（3）如果再放入一个同样的圆柱，水面高度又变成了多少分米？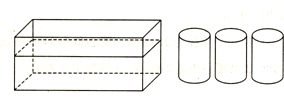

左边正方形的边长为4，右边正方形对角线长度为6．如果按照图中的方式旋转，那么得到的两个旋转体的体积之比是多少？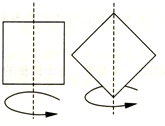

张大爷去年用长2米宽1米的长方形苇席围成容积最大的圆柱形粮囤，今年改用长3米宽2米的长方形苇席围成容积最大的圆柱形粮囤．今年粮囤的容积是去年粮囤容积的多少倍？

如图是一个棱长为4厘米的正方体，分别在前、后、左、右、上、下各面的中心位置挖去一个棱长1厘米的小正方体，做成一种玩具．该玩具的表面积是多少平方厘米？如果把这些洞都打穿，表面积又变成了多少？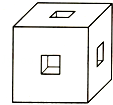

一个正方体被切成24个大小形状一模一样的小长方体（如图），这些小长方体的表面积之和为162平方厘米．请问：原正方体的体积是多少？

如图1，将一个棱长为10的正方体从顶点A切掉一个棱长为4的正方体，得到如图2的立体图形，这个立体图形的表面积是多少？如果再从顶点B切掉一个棱长为6的正方体，那么剩下的立体图形的表面积又是多少？

如图，有30个棱长为1米的正方体堆成一个四层的立体图形．请问：这个立体图形的表面积等于多少？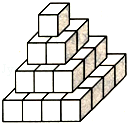

有一个高24厘米，底面半径为10厘米的圆柱形容器，里面装了一半水，现有一根长30厘米，底面半径为2厘米的圆柱体木棒．将木棒竖直放入容器中，使棒的底面与容器的底面接触，这时水面升高了多少厘米？

如图，一块三层蛋糕，由三个高都为1分米，底面半径分别为1.5分米、1分米和0.5分米的圆柱体组成．请问：
（1）这个蛋糕的表面积是多少平方分米？（л取3.14）
（2）如果沿经过中轴线AB的平面切一刀，将该蛋糕分成完全相同的两部分，那表面积之和又是多少？

（1）如图，将4块棱长为1的正方体木块排成一排，拼成一个长方体．那么拼合后这个长方体的表面积，比原来4个正方体的表面积之和少了多少？
（2）一个正方体形状的木块，棱长为1，如图所示，将其切成两个长方体，这两部分的表面积总和是多少？如果在此基础上再切4刀，将其切成大大小小共18块长方体．这18块长方体表面积总和又是多少？

如图是一个边长为2厘米的正方体．在正方体的上面的正中向下挖一个边长为1厘米的正方体小洞；接着在小洞的底面正中再向下挖一个边长为厘米的小洞；第三个小洞的挖法与前两个相同，边长为厘米．那么最后得到的立体图形的表面积是多少平方厘米？