小学数学质数与合数试题

在2、3、4、13、25、37、68、87、99这些数中，是质数的有　　　　　　，是合数的有　　　　　　．

（慈溪市）4只同样的瓶子分别装有一定数量的油，每瓶和其它各瓶分别合称一次，所得重量的千克数如下：8，9，10，11，12，13．已知这四只空瓶的重量之和以及油的质量之和都为质数．那么最重的两瓶内共有油多少千克？

写出10个连续自然数，它们个个都是合数．

两个质数的乘积一定是（    ）
A.奇数     B.合数     C.质数

在九个连续的自然数中，至多有多少个质数？

一个两位数，个位上和十位上的数都是合数，并且是互质数，这个数最大为（　　）
A．94     B．98     C．99

有三张卡片，在它们上面各写有一个数字2、3、7，从中至少取出一张组成一个数，其中有几个质数？请将它们写出来．

从1﹣9九个数中选取六个数，组成三个两位数的质数，并使这三个质数的和也是质数，并且和要尽可能小，这三个质数的和是      ．

将1到9这9个数字在算式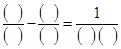的每一个括号内各填入一个数字，使得算式成立，并且要求所填每一个括号内数字均为质数?

已知P,Q都是质数，并且，则=        

炎黄骄子 菲尔兹奖被誉为“数学界的诺贝尔奖”，只奖励40岁以下的数学家．华人数学家丘成桐、陶哲轩分别于1982年、2006年荣获此奖．我们知道正整数中有无穷多个质数(素数)，陶哲轩等证明了这样一个关于质数分布的奇妙定理：对任何正整数k，存在无穷多组含有k个等间隔质数(素数)的数组．例如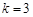，时，3，5，7是间隔为2的3个质数；5，11，17是间隔为6的3个质数：而       ，      ，       是间隔为12的3个质数(由小到大排列，只写一组3个质数即可)．

既是素数又是偶数的数是　　　　　　．

在自然数1﹣10中，　　　　　　是偶数但不是合数，　　　　　　是奇数但不是质数．

如图是某一个浅湖泊的平面图，图中曲线都是湖岸．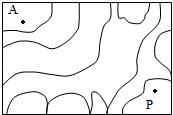

（1）若P点在岸上，则A点在岸上还是水中？
（2）某人过这湖泊，他下水时脱鞋，上岸时穿鞋．若有一点B，他脱鞋的次数与穿鞋的次数和是奇数，那么B点在岸上还是水中？说明理由．

求1-100中不能表示成两个合数的乘积再加一个合数的最大数是多少？