如图3-4所示，轻弹簧的一端固定在地面上，另一端与木块B相连。木块A放在B上。两木块质量均为
，竖直向下的力F作用在A上，A、B均静止，问：
（1）将力F瞬间撤去后，A、B共同运动到最高点，此时B对A的弹力多大？
（2）要使A、B不会分开、力F应满足什么条件？
如图3-18所示为一单摆的共振曲线，则该单摆的摆长约为多少？共振时单摆的振幅多大？共振时摆球简谐运动的最大加速度和最大速度大小各为多少？（
取10m/s2）
如图2-3所示，一带电粒子以竖直向上的初速度
，自A处进入电场强度为E、方向水平向右的匀强电场，它受到的电场力恰与重力大小相等。当粒子到达图中B处时，速度大小仍为，但方向变为水平向右，那么A、B之间的电势差等于多少？从A到B经历的时间为多长？
一内壁光滑的环形细圆管，位于竖直平面内，环的半径为R（比细管的半径大得多）。在圆管中有两个直径与细管内径相同的小球（可视为质点）。A球的质量为
，B球的质量为
，它们沿环形圆管顺时针运动，经过最低点时的速度为
，设A球运动到最低点时，B球恰好运动到最高点，证明：若要此时两球作用于圆管的合力为零，那么，，R与应满足的关系式是：
。
云室处在磁感应强度为B的匀强磁场中，一静止的质量为M的原于核在云室中发生一次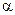
衰变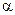，粒子的质量为
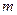，电量为q，其运动轨迹在与磁场垂直的平面内，现测得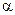粒子运动的轨道半径R，试求在衰变过程中的质量亏损。
已知物体从地球上的逃逸速度（第二宇宙速度）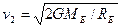
，其中G、ME、RE分别是引力常量、地球的质量和半径。已知G=6.7×10-11N·m2/kg2，c=3.0×108m/s，求下列问题：（1）逃逸速度大于真空中光速的天体叫做黑洞，设某黑洞的质量等于太阳的质量M=2.0×1030kg，求它的可能最大半径（这个半径叫Schwarhid半径）；（2）在目前天文观测范围内，物质的平均密度为10-27kg/m3，如果认为我们的宇宙是这样一个均匀大球体，其密度使得它的逃逸速度大于光在真空中的速度c，因此任何物体都不能脱离宇宙，问宇宙的半径至少多大？（最后结果保留两位有效数字）
有两只电压表A和B，量程已知，内阻不知等于多少；另有一节干电池，它的内阻不能忽略，但不知等于多少。只用这两只电压表、电键和一些连接用的导线，能通过测量计算这节电池的电动势（已知电动势不超出电压表的量程，干电池不许拆开）。
（1）画出你测量时所用的电路图；
（2）以测得的量作为已知量，导出计算电动势的式子。
一个电流、电压两用表的电路如图所示，小量程电流表G的量程是0.001A，内阻是100Ω，两个电阻的阻值是
，问：
（1）双刀双掷电键接到哪边是电流表，接到哪边是电压表？
（2）电流表、电压表的量程各是多大？
“加速度计”作为测定物体加速度的仪器，已被广泛地应用于飞机、潜艇、导弹、航天器等装置的制导中，如图所示是“应变式加速度计”的原理图。支架A、B固定在待测系统上，滑块穿在A、B间的水平光滑杆上，并用轻弹簧固接于支架A上，其下端的滑动臂可在滑动变阻器上自由滑动.随着系统沿水平方向做变速运动，滑块相对于支架发生位移，并通过电路转换为电信号从1、2两接线柱输出。
已知滑块质量为m，弹簧劲度系数为k，电源电动势为E，内电阻为r，滑动变阻器总阻值R=4r，有效总长度为L。当待测系统静止时，滑动臂P位于滑动变阻器的中点，且1、2两接线柱输出的电压U0=0.4E。取AB方向为参考正方向。
（1）写出待测系统沿AB方向做变速运动的加速度a与 “1、2”两接线柱间的输出电压U间的关系式；
（2）确定该“加速度计”的测量范围。
如图所示的电路中，电源电动势
，其内阻可忽略不计。电阻的阻值分别为
，电容器的电容
。闭合开关S，待电流稳定后，用电压表测
两端电压，其稳定值为
。
（1）该电压表的内阻为多大？
（2）由于电压表的接入，电容器的带电量变化了多少？
如图所示，电阻R3＝4Ω，电表为理想表，开始时R1、R2、R3中都有电流通过，电压表示数为2V，电流表示数为0.75A，后来三个电阻中有一个发生断路，使电压表示数变为3.2V，电流表示数变为0.8A。
（1）哪个电阻断路？
（2）求电阻R1、R2的阻值各为多少？
（3）电源电动势和内阻各为多少？
如图所示，一质量为m的砂袋用长为l的绳子拴住悬挂在O点，被拳击运动员水平击中后，荡起的最大高度是h.求砂袋刚被击中后的瞬间，砂袋的向心加速度是多大?
，求经过多长时间两小球速度方向间的夹角为90°？
粤公网安备 44130202000953号