高中物理α粒子散射实验试题

如图所示，在x轴的上方（y＞0的空间内）存在着垂直于纸面向里、磁感应强度为B的匀强磁场，一个不计重力的带正电粒子从坐标原点O处以速度v进入磁场，粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成45°角，若粒子的质量为m，电量为q，则（1）该粒子在磁场中作圆周运动的轨道半径为          ；（2）粒子在磁场中运动的时间为           ；（3）该粒子射出磁场的位置坐标为                。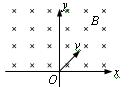

如图所示的坐标平面内,在y轴的左侧存在垂直纸面向外、磁感应强度大小B₁=0.20T的匀强磁场,在y轴的右侧存在垂直纸面向里、宽度d=0.125m的匀强磁场B₂.某时刻一质量m=2.0×10^-8kg、电量q=+4.0×10^-4C的带电微粒（重力可忽略不计）,从x轴上坐标为（-0.25m,0）的P点以速度v=2.0×10³ m/s沿y轴正方向运动.试求:

（1）微粒在y轴的左侧磁场中运动的轨道半径;
（2）微粒第一次经过y轴时速度方向与y轴正方向的夹角;
（3）要使微粒不能从右侧磁场边界飞出,B₂应满足的条件

阿尔法磁谱仪用于探测宇宙中的反物质和暗物质（即由“反粒子”构成的物质），如氚核（）的反粒子为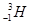（）。该磁谱仪核心部分截面区域是半径为r的圆形磁场，磁场方向垂直纸面向外，如图所示，P为入射窗口，各粒子从P射入速度相同，均沿直径方向，Pabcde为圆周上等分点，如反质子射入后打在e点，则氚核粒子射入将打在(  )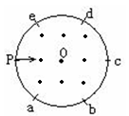

A．a

B．b

C．d

D．c

如右图所示，有界匀强磁场边界线SP//MN，速率不同的同种带电粒子（重力不计）从S 点沿SP方向同时射入磁场。其中穿过a点的粒子速度v₁与MN垂直，穿过b点的粒子速度v₂与MN成60°角，设两粒子从S到a、b所需时间分别为t₁和t₂。
（1）在图上画出两粒子的运动轨迹；
（2）求v₁:v₂；
（3）求t₁:t₂。

如图所示，NM的上侧有匀强磁场，磁场方向垂直于纸面向里，磁感应强度的大小为B。一带负电的粒子（不计重力）从P处以垂直于MN的初速度射入磁场区域，最后通过点。已知此粒子的比荷，求：
（1）P间的距离L？
（2）粒子从P运动到需要多长的时间？

如图所示，直角三角形ABC区域中存在一匀强磁场，比荷相同的两个粒子沿AB方向射入磁场，

2,4,6

分别从AC边上的P、Q两点射出，则

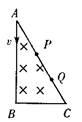
A．从P射出的粒子速度大

B．从Q射出的粒子速度大

C．从P射出的粒子，在磁场中运动的时间长

D．两粒子在磁场中运动的时间一样长

如图所示，在x＜0与x ＞0的区域中，存在磁感应强度大小分别为B₁与B₂的匀强磁场，磁场方向均垂直于纸面向里，且B₁＞B₂。一个带负电荷的粒子从坐标原点O以速度V沿x轴负方向射出，要使该粒子经过一段时间后又经过O点，B₁与B₂的比值应满足什么条件？

 
 
 
 

如图所示，磁感应强度B.电荷运动的速度v和磁场对电荷的作用力F的方向的相互关系正确的是（四幅图中B.v、F方向都是两两垂直）

如图所示，一束带电粒子沿水平方向沿虚线飞过磁针上方，并与磁针方向平行，能使磁针N极转向读者，那么这束带电粒子可能是（     ）

A．向右飞的正离子	B．向左飞的负离子
C．向右飞的负离子	D．向左飞的正离子

在以坐标原点为中心、边长为L的正方形EFGH区域内，存在磁感应强度为B、方向垂直于纸面向里的匀强磁场，如图所示。在A处有一个粒子源，可以连续不断的沿-x方向射入速度不同的带电粒子，且都能从磁场的上边界射出。已知粒子的质量为m，电量大小为q，重力不计，不考虑粒子间的相互作用。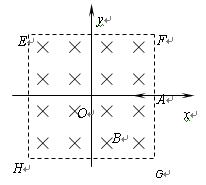

（1）试判断粒子的电性；
（2）求从F点射出的粒子在磁场中运动的时间；
（3）若粒子以速度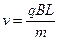射入磁场，求粒子由EF边射出时的位置坐标。

如图所示，在第二象限的正方形区域Ⅰ内分别存在着垂直纸面向里的匀强磁场；在第四象限区域Ⅱ存在着垂直纸面向外的无限大的匀强磁场，两磁场的磁感应强度均为B，方向相反。一质量为m、电量为e电子由P(－d，d)点，沿x轴正方向射入磁场区域Ⅰ。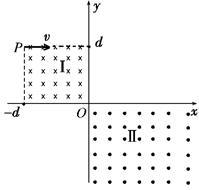

(1)求电子能从第三象限射出的入射速度的范围；
(2)若电子从(0，d/2)位置射出，求电子离开磁场Ⅱ时的位置与坐标原点O的距离。

如图所示，圆形区域内有垂直于纸面向里的匀强磁场，一个带电粒子以速度从点沿直径方向射入磁场，经过时间从点射出磁场，与成60°角。现将带电粒子的速度变为/3，仍从点沿原方向射入磁场，不计重力，则粒子在磁场中的运动时间变为   (     )

A．

B．2

C．

D．3

如图所示，在半径为R的圆内有一磁感应强度为B的向外的匀强磁场，一质量为m、电荷量为q的粒子（不计重力），从A点对着圆心方向垂直射入磁场，从C点飞出，则（   ）

A．粒子带负电

B．粒子的轨道半径为R

C．带电粒子从C点飞出时，速度偏转角为120°

D．粒子在磁场中运动的时间为

如图所示，在X轴上方有匀强磁场B，一个质量为，带电荷量为的粒子，以速度从O点射入磁场，角已知，粒子重力不计，求：
(1)粒子在磁场中运动的时间；
(2)粒子离开磁场的位置与O点间的距离。

1998年6月2日，我国科学家研制的阿尔法磁谱仪由“发现号”航天飞机搭载升空，用于探测宇宙中的反物质和暗物质（即反粒子）——，如₁³H反粒子_-1³H．该磁谱仪核心部分截面区域是半径为r的圆形磁场，P为入射窗口，各粒子从P射入速度相同，均直径方向，Pabcde为圆周上等分点，如反质子射入后打在a点，则反氘核粒子射入将打在何处，具偏转角多少？