高中物理α粒子散射实验试题

一足够长的矩形区域abcd内充满磁感应强度为B，方向垂直纸面向里的匀强磁场，矩形区域的左边界ad宽为L，现从ad中点O垂直于磁场射入一带电粒子，速度大小为v₀方向与ad边夹角为30°，如图所示。已知粒子的电荷量为q，质量为m（重力不计）。

（1）若粒子带负电，且恰能从d点射出磁场，求v₀的大小；  

（2）若粒子带正电，使粒子能从ab边射出磁场，求v₀的取值范围以及在该范围内粒子在磁场中运动时间t的范围。

如图所示，在xOy坐标系的第一象限中有一半径为r＝0.1 m的圆形磁场区域，磁感应强度B＝1 T，方向垂直纸面向里，该区域同时与x轴、y轴相切，切点分别为A、C.现有大量质量为1×10^－18 kg（重力不计），电量大小为2×10^－10 C，速率均为2×10⁷m/s的带负电的粒子从A处垂直磁场进入第一象限，速度方向与y轴夹角为θ，且0<θ<180°，则下列说法错误的是(   )

A．粒子的轨迹圆和磁场圆的半径相等
B．这些粒子轨迹圆的圆心构成的圆和磁场圆的半径相等
C．部分粒子的运动轨迹可以穿越坐标系进入第2象限
D．粒子的轨迹可以覆盖整个磁场圆

如图所示，带箭头的实线表示电场中电场线的分布情况，一带电粒子在电场中运动轨迹如图中的虚线所示，粒子只受电场力，则正确的说法是

A．若粒子是从a点到b点，则带正电

B．粒子肯定带负电

C．若粒子是从b点到a点，则加速度减小

D．若粒子是从b点到a点，则速度减小

如图所示，直角三角形ABC区域中存在一匀强磁场，比荷相同的两个粒子（不计重力）沿AB方向射入磁场，分别从AC边上的P、Q两点射出，则（  ）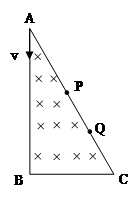

A．从P点射出的粒子速度大

B．从Q点射出的粒子速度大

C．从Q点射出的粒子在磁场中运动的时间长

D．两个粒子在磁场中运动的时间一样长

如图是某离子速度选择器的原理示意图，在一半径为R 的绝缘圆柱形筒内有磁感应强度为B的匀强磁场，方向平行于轴线．在圆柱形筒上某一直径两端开有小孔M、N，现有一束速率不同、比荷均为k的正、负离子，从M孔以α角入射，一些具有特定速度的离子未与筒壁碰撞而直接从N孔射出(不考虑离子间的作用力和重力)．则从N孔射出的离子(　　)

A．是正离子，速率为kBR/cos α

B．是正离子，速率为kBR/sin α

C．是负离子，速率为kBR/sin α

D．是负离子，速率为kBR/cos α

如图所示，在x轴上方存在垂直于纸面向里的匀强磁场，磁感应强度为B.在xOy平面内，从原点O处沿与x轴正方向成θ角(0＜θ＜π)以速率v发射一个带正电的粒子(重力不计)．则下列说法正确的是(　　)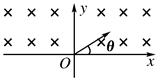

A．若θ一定，v越大，则粒子在磁场中运动的时间越短
B．若θ一定，v越大，则粒子在磁场中运动的角速度越大
C．若v一定，θ越大，则粒子在磁场中运动的时间越短
D．若v一定，θ越大，则粒子在离开磁场的位置距O点越远

在如图所示的直角坐标系中，x轴的上方存在与x轴正方向成45°角斜向右下方的匀强电场，场强的大小为E＝×10⁴ V/m.x轴的下方有垂直于xOy面向外的匀强磁场，磁感应强度的大小为B＝2×10^－2 T．把一个比荷为＝2×10⁸ C/kg的正电荷从坐标为(0,1)的A点处由静止释放．电荷所受的重力忽略不计．

(1)求电荷从释放到第一次进入磁场时所用的时间；
(2)求电荷在磁场中做圆周运动的半径；(保留两位有效数字)
(3)当电荷第二次到达x轴时，电场立即反向，而场强大小不变，试确定电荷到达y轴时的位置坐标．

如图，在区域I分布有沿-y方向的匀强电场，场强大小为为E,区域II分布有垂直xoy向里的匀强磁场，磁感应强度为B，两区宽度相同，有一个质子从I区的左侧垂直边界入射，恰好垂直II区右边界射出，求质子的入射速度。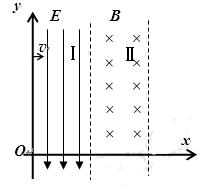

如图所示，MN表示真空室中垂直于纸面放置的感光板，它的一侧有匀强磁场，磁场方向垂直于纸面向里，磁感应强度大小为B. 一个电荷量为q的带电粒子从感光板上的狭缝O处以垂直于感光板的初速度v射入磁场区域，经一次偏转到达P点. 经测量P、O间的距离为l，不计带电粒子受到的重力. 求：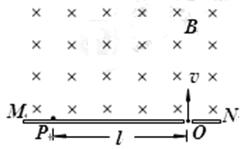

（1）带电粒子所受洛伦兹力的大小；
（2）带电粒子的质量。

如图，在矩形区域abcd区域中，分布有垂直纸面向外的匀强磁场，ab长为L,在ab的中点P处有一电子发射源，出射电子速率取一切可能值，所有电子出射的速度方向均与ab成30°，下列说法正确的是(       )

A．只要初速度大小取合适的值，电子可以在磁场中做完整的圆周运动

B．电子入射速度越大，在磁场中运动的时间一定越短

C．从ad边出射的电子一定比从bc出射的粒子时间长

D．当时，cd边无电子射出

如图所示、相互垂直，将空间分成两个区域，．区域Ⅰ中有垂直于纸面向外的匀强磁场，区域Ⅱ中有平行于，大小为的匀强电场和另一未知匀强磁场（方向垂直纸面，图中未画出）．一束质量为、电量为的粒子以不同的速率（速率范围0~）自点垂直于射入区域Ⅰ．其中以最大速率射入的粒子恰能垂直于进入区域Ⅱ．已知间距为，不计粒子重力以及粒子间的相互作用．试求：

（1）区域Ⅰ中匀强磁场的磁感应强度大小；
（2）为使速率为的粒子进入区域Ⅱ后能沿直线运动，则区域Ⅱ的磁场大小和方向；
（3）分界线上，有粒子通过的区域的长度．

如图所示，半径为R的圆形区域内、外有方向相反的与圆平面垂直的匀强磁场，圆形区域外的匀强磁场范围足够大，磁感应强度大小均为B．一质量为m、电量为q的带正电粒子从圆弧上P点正对圆心O以速度v进入圆形区域内的磁场，经过时间从Q点进入圆形区域外的磁场，不计粒子重力．求：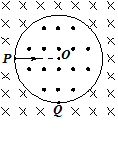

（1）粒子在圆形区域内的磁场中做匀速圆周运动的半径r；
（2）粒子从P点开始经Q点回到P点的最短时间t₂；
（3）若粒子从P点以速度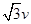正对圆心O进入圆形区域内的磁场，则粒子是否能在圆形区域内、外磁场中做周期性运动，如果不能，请说明理由；如果能，试求出这个周期．

(8分)如图所示，直线MN上方为磁感应强度为B的足够大的匀强磁场．一电子(质量为m、电荷量为e)，以v的速度从点O与MN成30°角的方向射入磁场中，求：
(1)电子从磁场中射出时距O点多远；
(2)电子在磁场中运动的时间为多少．

如图所示，在竖直平面内有一边界半径为R的圆形匀强磁场区域，磁感应强度为B，方向垂直纸面向里．一质量为m、电量为q的负点电荷从圆边缘的P点沿直径方向进入匀强磁场中，射出磁场时速度方向偏转了60°．不计点电荷的重力．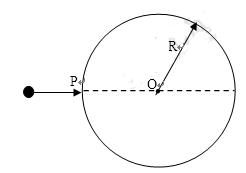

(1)求点电荷速度υ的大小?
(2)如果点电荷速度大小不变，以不同方向从P点进入圆形匀强磁场区域，点电荷在磁场中运动时间不同，求点电荷在磁场中运动的最长时间?

如图所示，ABC为与匀强磁场垂直的边长为的等边三角形，比荷为的电子以速度₀从A点沿AB边出射，欲使电子经过BC边，则磁感应强度B的取值为 [     ]

A．	B．
C．	D．