如图所示，两块相距为d的水平放置的金属板组成一个平行板电容器，用导线、开关S将其与一个n匝的线圈连接，线圈置于方向竖直向上的均匀变化的磁场中，两板间放一台小压力传感器，压力传感器上表面绝缘且水平，在其上表面静止放置一个质量为m、电荷量＋q的小球。已知S断开时传感器上有示数，S闭合后传感器上的示数变为原来的二倍，则穿过线圈的磁场的磁感应强度变化情况和磁通量变化率分别是( )
A．正在增强， ＝ |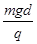
B．正在增强，＝ |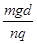
| C．正在减弱，＝ |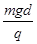
D．正在减弱，＝ |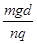
如图所示，矩形闭合线圈abcd竖直放置， OO’是它的对称轴，通电直导线AB与OO’平行，且AB、OO’所在平面与线圈平面垂直．如要在线圈中形成方向为abcda的感应电流，可行的做法是 （ ）
（A）AB中电流I逐渐增大
（B）AB中电流I先增大后减小
（C）AB中电流I正对OO’靠近线圈
（D）线圈绕OO’轴逆时针转动90°（俯视）
如图所示，环形导线中通有顺时针方向的电流I，则该环形导线中心处的磁场方向为 ( )
| A．水平向右 |
| B．水平向左 |
| C．垂直于纸面向里 |
| D．垂直于纸面向外 |
(19分)如图所示的平行板之间，存在着相互垂直的匀强磁场和匀强电场，磁场的磁感应强度B1＝0.20 T，方向垂直纸面向里，电场强度E1＝1.0×105 V/m，PQ为板间中线．紧靠平行板右侧边缘xOy坐标系的第一象限内，有一边界线AO，与y轴的夹角∠AOy＝45°，边界线的上方有垂直纸面向外的匀强磁场，磁感应强度B2＝0.25 T，边界线的下方有水平向右的匀强电场，电场强度E2＝5.0×105 V/m，在x轴上固定一水平的荧光屏．一束带电荷量q＝8.0×10－19C、质量m＝8.0×10－26 kg的正离子从P点射入平行板间，沿中线PQ做直线运动，穿出平行板后从y轴上坐标为(0,0.4 m)的Q点垂直y轴射入磁场区，最后打到水平的荧光屏上的位置C.求：
(1)离子在平行板间运动的速度大小．
(2)离子打到荧光屏上的位置C的坐标．
(3)现只改变AOy区域内磁场的磁感应强度大小，使离子都不能打到x轴上，磁感应强度大小B2′应满足什么条件？
如图甲所示，在水平面上固定有长为、宽为
的金属"
"型轨导，在"
"型导轨右侧
范围内存在垂直纸面向里的匀强磁场，且磁感应强度随时间变化规律如图乙所示。在
时刻，质量为
的导体棒以
的初速度从导轨的左端开始向右运动，导体棒与导轨之间的动摩擦因数为
，导轨与导体棒单位长度的电阻均为
，不计导体棒与导轨之间的接触电阻及地球磁场的影响（取
）。
（1）通过计算分析内导体棒的运动情况；
（2）计算内回路中电流的大小，并判断电流方向；
（3）计算内回路产生的焦耳热。
如下图（a）所示，间距为l、电阻不计的光滑导轨固定在倾角为θ的斜面上。在区域I内有方向垂直于斜面的匀强磁场，磁感应强度为B；在区域Ⅱ内有垂直于斜面向下的匀强磁场，其磁感应强度Bt的大小随时间t变化的规律如下图（b）所示。t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑，同时下端的另一金属细棒cd在位于区域I内的导轨上由静止释放。在ab棒运动到区域Ⅱ的下边界EF处之前，cd棒始终静止不动，两棒均与导轨接触良好。已知cd棒的质量为m、电阻为R，ab棒的质量、阻值均未知，区域Ⅱ沿斜面的长度为2l，在t=tx时刻（tx未知）ab棒恰进入区域Ⅱ，重力加速度为g。求：
通过cd棒电流的方向和区域I内磁场的方向；
当ab棒在区域Ⅱ内运动时cd棒消耗的电功率；
ab棒开始下滑的位置离EF的距离；
ab棒开始下滑至EF的过程中回路中产生的热量。
如图所示，面积为S的矩形线圈共N匝，线圈总电阻为R，在磁感应强度为B、方向垂直纸面向里的匀强磁场中以竖直线OO′为轴，以角速度
，匀速旋转，图示位置C与纸面共面，位置A与位置C成45°角。线圈从位置A转过90°到达位置B的过程中，下列说法正确的是（ ）
A．平均电动势为
B．通过线圈某一截面的电量q=0
C．为保证线圈匀速旋转，外界须向线圈输入的能量应为
D．在此转动过程中，电流方向并未发生改变
如图4所示，边长相等的正方形导体框与正方形匀强磁场区的对角线在同一水平线上，导体框沿水平方向匀速通过垂直于纸面向外的磁场区，导体框中的电流随时间变化关系正确的是(顺时针方向电流为正)( )．
如图所示，在匀强磁场中匀速转动的矩形线圈的周期为T,转轴O1O2垂直于磁场方向，线圈电阻为2
。从线圈平面平行磁场方向平行时开始计时，线圈转过60°时的感应电 流为1A。那么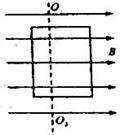
A．线圈消耗的电功率为8W
B．线圈中感应电流的有效值为2A
C．任意时刻穿过线圈的磁通量为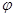
=
sin
D．任意时刻线圈中的感应电动势为e=4cos
电阻可忽略的光滑平行金属导轨长S=1.15m，两导轨间距L="0.75" m，导轨倾角为30°，导轨上端ab接一阻值R=1.5Ω的电阻，磁感应强度B=0.8T的匀强磁场垂直轨道平面向上。阻值r=0.5Ω，质量m=0.2kg的金属棒与轨道垂直且接触良好，从轨道上端ab处由静止开始下滑至底端，在此过程中金属棒产生的焦耳热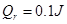
。(取
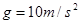)求：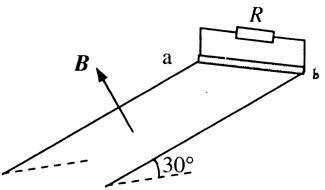
(1)金属棒在此过程中克服安培力的功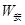
；
(2)金属棒下滑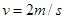速度
时的加速度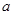
．
(3)为求金属棒下滑的最大速度
，有同学解答如下：由动能定理
，……。由此所得结果是否正确？若正确，说明理由并完成本小题；若不正确，给出正确的解答。
如图所示，A为水平放置的胶木圆盘，在其侧面带有负电荷，在A的正上方用丝线悬挂一个金属圆环B，使B的环面在水平面上且与圆盘面平行，其轴线与胶木盘A的轴线
重合。现使胶木盘A由静止开始绕其轴线OO′按箭头所示方向加速转动，则( )
| A．金属环B的面积有扩大的趋势，丝线受到的拉力增大 |
| B．金属环B的面积有缩小的趋势，丝线受到的拉力减小 |
| C．金属环B的面积有扩大的趋势，丝线受到的拉力减小 |
| D．金属环B的面积有缩小的趋势，丝线受到的拉力增大 |
如图甲所示，不计电阻的平行金属导轨与水平夹角37°放置，导轨间距为L＝1 m，上端接有电阻R＝3 Ω，虚线OO′ 下方是垂直于导轨平面的匀强磁场．现将质量m＝0.1 kg、电阻r＝1 Ω的金属杆ab从OO′上方某处垂直导轨由静止释放，杆下滑过程中始终与导轨垂直并保持良好接触，杆下滑过程中的v－t图象如图乙所示．(取g＝10 m/s2)
求：(1)磁感应强度B；
(2)杆在磁场中下滑0.1s过程中电阻R产生的热量．
有人设计了一种可测速的跑步机，测速原理如题23图所示，该机底面固定有间距为
、长度为
的平行金属电极。电极间充满磁感应强度为
、方向垂直纸面向里的匀强磁场，且接有电压表和电阻
,绝缘橡胶带上镀有间距为的平行细金属条，磁场中始终仅有一根金属条，且与电极接触良好，不计金属电阻，若橡胶带匀速运动时，电压表读数为
,求：
⑴橡胶带匀速运动的速率；
⑵电阻R消耗的电功率；
⑶一根金属条每次经过磁场区域克服安培力做的功。
如图所示的器材可用来研究电磁感应现象及判定感应电流的方向。但给出的实物图中连接并不完整，请你试着连成完整的实验电路基础上回答：若将线圈L1插入线圈L2中，合上开关S，能使线圈L2中感应电流的磁场方向与线圈L1中原磁场方向相同的实验操作是（ ）
| A．插入铁芯F | B．拔出线圈L1 |
| C．使变阻器阻值R变大 | D．断开开关S |
粤公网安备 44130202000953号