高中物理用多用电表测电阻试题

某同学想要了解导线在质量相同时，电阻与截面积的关系，选取了材料相同、质量相等的5卷导线，进行了如下实验：

1.(1)用螺旋测微器测量某一导线的直径如下图所示，读得直径＝．

（2)该同学经实验测量及相关计算得到如下数据：

电阻	121.0	50.0	23.9	10.0	3.1
导线直径	0.80l	0.999	1.20l	1.494	1.998
导线截面积	0.504	0.784	1.133	1.753	3.135

请你根据以上数据判断，该种导线的电阻与截面积是否满足反比关系?若满足反比关系，请说明理由；若不满足，请写出与应满足的关系．

2.(3)若导线的电阻率，则表中阻值为的导线长度=(结果保留两位有效数字)

如图所示，厚薄均匀的矩形金属薄片边长ab="10" cm，bc="5" cm，当将A与B接入电压为U的电路中时，电流强度为1 A，若将C与D接入电压为U的电路中，则电流为

A．4A	B．2A
C．A	D．A

一个标有“220V　　60W”的白炽灯泡，当用多用电表的欧姆挡去测量它的电阻时，其阻值

A．接近于807Ω	B．接近于0Ω
C．明显大于807Ω	D．明显小于807Ω

关于电阻率，下列说法中不正确的是

A．电阻率是表征材料导电性能好坏的物理量，电阻率越大，其导电性能越好

B．各种材料的电阻率都与温度有关，金属的电阻率随温度的升高而增大

C．所谓超导体，当其温度降低到接近绝对零度的某个临界温度时，它的电阻率突然变为零

D．某些合金的电阻率几乎不受温度变化的影响，通常用它们制作标准电阻

材料的电阻率ρ随温度变化的规律为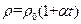，其中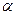称为电阻温度系数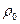，是材料在t="0" ℃时的电阻率，在一定的温度范围内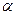是与温度无关的常量。金属的电阻一般随温度的增加而增加，有正温度系数；而某些非金属如碳等则相反，具有负温数系数。利用具有正负温度系数的两种材料的互补特性，可制成阻值在一定温度范围内不随温度变化的电阻。已知：在0 ℃时，铜的电阻率为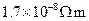，碳的电阻率为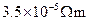，在0 ℃附近，铜的电阻温度系数为3.9×10^–3 ℃^-1,碳的电阻温度系数为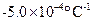。将横截面积相同的碳棒与铜棒串接成长1.0 m的导体，要求其电阻在0 ℃附近不随温度变化，求所需碳棒的长度(略碳棒和铜棒的尺寸随温度的变化).

导体的电阻是导体本身的一种性质，对于同种材料的导体，下列表述正确的是（）

A．	横截面积一定，电阻与导体的长度成正比
B．	长度一定，电阻与导体的横截面积成正比
C．	电压一定，电阻与通过导体的电流成正比
D．	电流一定，电阻与导体两端的电压成反比

材料的电阻率随温度变化的规律为，其中称为电阻温度系数，是材料在时的电阻率。在一定的温度范围内是与温度无关的常量。金属的电阻一般随温度的增加而增加，具有正温度系数；而某些非金属如碳等则相反，具有负温度系数。利用具有正负温度系数的两种材料的互补特性，可制成阻值在一定温度范围内不随温度变化的电阻。已知：在时，铜的电阻率为，碳的电阻率为；在附近，铜的电阻温度系数为，碳的电阻温度系数为。将横截面积相同的碳棒与铜棒串接成长的导体，要求其电阻在附近不随温度变化，求所需碳棒的长度（忽略碳棒和铜棒的尺寸随温度的变化）。