如图1所示,厚度均匀的矩形金属薄片边长ab=10 cm,bc=5 cm.当将A与B接入电压为U的电路中时,电流为1 A;若将C与D接入同一电路中,则电流为 ( ) 
| A.4 A | B.2 A | C. A A |
D. A A |
某同学将一直流电源的总功率PE、输出功率PR和电源内部的发热功率Pr随电流I变化的图线画在了同一坐标系中,如图中的a、b、c所示.则判断错误的是( )
| A.直线a表示电源的总功率 |
| B.曲线c表示电源的输出功率 |
| C.电源的电动势E=3 V,内电阻r=1 Ω |
| D.电源的最大输出功率Pm=9 W |
24.(15分)材料的电阻率ρ随温度变化的规律为ρ=ρ0(1+at),其中α称为电阻温度系数,ρ0是材料在t="0" ℃时的电阻率.在一定的温度范围内α是与温度无关的常数。金属的电阻一般随温度的增加而增加,具有正温度系数;而某些非金属如碳等则相反,具有负温数系数.利用具有正负温度系数的两种材料的互补特性,可制成阻值在一定温度范围内不随温度变化的电阻.已知:在0 ℃时,铜的电阻率为1.7×10 –8Ω•m,碳的电阻率为3.5×10 -5Ω•m,附近,在0 ℃时,.铜的电阻温度系数为3.9×10 –3 ℃-1,碳的电阻温度系数为-5.0×10-4℃-1.将横截面积相同的碳棒与铜棒串接成长1.0 m的导体,要求其电阻在0 ℃附近不随温度变化,求所需碳棒的长度(忽略碳棒和铜棒的尺寸随温度的变化).
.导体的电阻是导体本身的一种性质,对于同种材料的导体,下列表述正确的是( )
| A.横截面积一定,电阻与导体的长度成正比 |
| B.长度一定,电阻与导体的横截面积成正比 |
| C.电压一定,电阻与通过导体的电流成正比 |
| D.电流一定,电阻与导体两端的电压成反比 |
A、B两根粗细相同的不同导线,电阻率之比1:2,长度之比为4:1,则它们的电阻之比RA:RB="__________" ;然后分别加上相同的电压,相同时间内通过两导线横截面的电荷量之比qA:qB=__________;消耗的电功率之比PA:PB=__________。
下列方法有可能使半导体材料的电阻率减小的是( )
| A.升高半导体的温度 | B.用光照射半导体 |
| C.在半导体中加入微量其他杂质 | D.以上情况都不可能 |
欧姆不仅发现了欧姆定律,还研究了电阻定律。有一个长方体金属电阻,材料分布均匀,边长分别为a、b、c,且a>b>c。电流沿以下方向流过该金属电阻,其中电阻阻值最小的是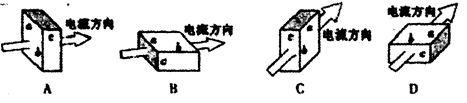
R1和 R2是材料相同,厚度相同,表面都为正方形的导体,但R1的尺寸比R2大得多,把它们分别连接在如图电路的A、B端,接R1时电压表的读数为U1,接R2时电压表的读数为U2 ,下列判断正确的是 A.R1= R2
A.R1= R2
B.R1 > R2
C.U1 < U2
D.U1= U2
均匀的电阻丝,在温度不变的情况下,下列情况中其电阻值不变的是( )
| A.长度不变,横截面积增大一倍 | B.横截面积不变,长度增大一倍 |
| C.长度和横截面半径都增大一倍 | D.长度和横截面面积都缩小一半 |
.下列说法正确的是:
| A.由E = F/q知,若q减半,则该处的场强变为原来的2倍 |
| B.由E = kQ/r2知,E与Q成正比,与r平方成反比 |
| C.电阻率表征了材料导电能力的强弱,由导体的材料决定, 且与温度有关 |
| D.导体的电阻跟导体两端电压成正比,跟导体中的电流成反比 |
有三根电阻丝,它们的长度、横截面积、电阻率分别如下表所示:
| 电阻 |
电阻丝长度 |
横截面积 |
电阻率 |
| R1 |
L |
S |
2ρ |
| R2 |
L |
2S |
ρ |
| R3 |
2L |
S |
2ρ |
则阻值最大的电阻丝是
A.R1 B.R2 C.R3 D.三根电阻丝的阻值一样大
第II卷(非选择题 共31分)
一根粗细均匀的导线,两端加上电压U时,通过导线中的电流强度为I,导线中自由电子定向移动的平均速度为v,若导线均匀拉长,使其半径变为原来的 ,再给它两端加上电压U,则( )
,再给它两端加上电压U,则( )
A.通过导线的电流为 |
B.通过导线的电流为 |
C.自由电子定向移动的平均速率为 |
D.自由电子定向移动的平均速率为 |
有三根电阻丝,它们的长度、横截面积、电阻率分别如下表所示:
| 电阻 |
电阻丝长度 |
横截面积 |
电阻率 |
| R1 |
L |
S |
2ρ |
| R2 |
L |
2S |
ρ |
| R3 |
2L |
S |
2ρ |
则阻值最大的电阻丝是( )
A.R1 B.R2 C.R3 D.三根电阻丝的阻值一样大
关于导体的电阻,下列说法正确的是:
| A.导体的电阻仅由导体两端的电压决定 |
| B.导体的电阻在一定温度下仅由长度和横截面积决定 |
| C.导体的电阻在一定温度下由导体的长度、粗细及材料决定 |
| D.导体的电阻与导体所通电流的大小有关 |