下列说法正确的是
| A.半导体材料导电性能不受外界条件的影响 |
| B.超导现象就是在温度降到某一临界值时电阻率突然降为零的现象 |
C.由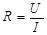 可知,R与导体两端电压U成正比,与通过导体的电流I成反比 可知,R与导体两端电压U成正比,与通过导体的电流I成反比 |
| D.由ρ= RS/L可知,ρ与S成正比,与L成反比 |
鸟儿落在110 kV的高压输电线上,虽然通电的高压线是裸露电线,但鸟儿仍然安然无恙。这是因为( )
| A.鸟有耐高压的天性 |
| B.鸟脚是干燥的,所以鸟体不导电 |
| C.鸟两脚间的电压几乎为零 |
| D.鸟体电阻极大,所以无电流通过 |
关于导体的电阻及电阻率的说法中,正确的是( )
| A.导体对电流的阻碍作用叫做导体的电阻,因此,只有导体有电流通过时,才具有电阻 |
| B.由R=可知,导体的电阻跟导体两端的电压成正比,跟导体中的电流成反比 |
| C.将一根导线一分为二,则半根导线的电阻和电阻率都是原来的二分之一 |
| D.某些金属、合金和化合物的电阻率随温度降低会突然减小为零,这种现象叫做超导现象 |
两根完全相同的金属裸导线,如果把其中一根均匀拉长到原来的2倍,把另一根对折后绞起来,则它们的电阻之比为( )
A. |
B. |
C. |
D. |
人们发现,大多数金属在温度降到某一数值时,都会出现电阻突然为零的现象,我们把这个现象称为 现象,如果采用这种电阻为零的金属做成输电线来进行输电,则在输电过程中输电线上消耗的电能为 .
有两个同种材料制成的导体,两导体为横截面为正方形的柱体,柱体高均为h,大柱体柱截面边长为a,小柱体柱截面边长为b,现将大小柱体串联接在电压U上,已知通过导体电流方向如图,大小为I,则导体电阻率为
A.ρ= |
B.ρ= |
C.ρ= |
D.ρ= |
(理)、下列关于电阻率的说法中,错误的是:
| A.电阻率只是一个比例常数,与任何其他因素无关 |
| B.电阻率反映材料导电性能的好坏,所以与材料有关 |
| C.电阻率与导体的温度有关 |
| D.电阻率在国际单位制中的单位是欧姆米 |
如图所示,R1和R2是材料相同、厚度相同,表面积为正方形的导体,已知R1的表面积是R2的100倍,通过导体的电流方向如图所示。则这两个导体的电阻关系为 ( )
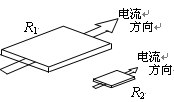
| A.R1=100R2 | B.R2=100R1 |
| C.R2=10R1 | D.R1=R2 |
A、B两地间铺有通讯电缆,长为L,它是由两条并在一起彼此绝缘的均匀导线组成的,通常称为双线电缆,在一次事故中经检查断定是电缆上某处的绝缘保护层损坏,导致两导线之间漏电,相当于该处电缆的两导线之间接入一个电阻.检查人员经过下面的测量可以确定损坏的位置:(1)令B端双线断开,在A处测出双线两端的电阻RA;(2)A端双线断开,在B处测出双线两端的电阻RB;(3)在A端的双线间加一已知电压UA,在B端的双线间用内阻很大的电压表测量出两线间的电压UB.
试由以上测量结果确定损坏处的位置.
如图(甲)是“测定电源电动势和内阻”实验的电路图,根据实验测得的几组I、U数据作出U—I图象如图(乙)所示,由图象可确定:该电源的电动势为 V,电源的内电阻为 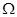 (计算结果保留两位有效数字).
(计算结果保留两位有效数字).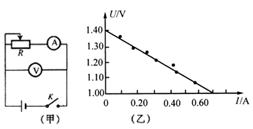
用20分度的游标卡尺测量某物体的长度如图甲所示,可知其长度为 cm;用螺旋测微器测量某圆柱体的直径如图乙所示,可知其直径为 mm.

某同学在测定金属圆柱体电阻率时需要先测量其尺寸,他分别使用游标卡尺和螺旋测微器测量圆柱体的长度和直径,某次测量的示数如图 (a)和如图(b)所示,则:长度为 cm,直径为 mm.
|


“测定金属的电阻率”的实验中,以下操作中错误的是( )
| A.用米尺测量金属丝的全长,且测量三次,算出其平均值,然后再将金属丝接入电路中 |
| B.用螺旋测微器在金属丝三个不同部位各测量一次直径,算出其平均值 |
| C.用伏安法测电阻时采用电流表内接法,多次测量后算出平均值 |
| D.实验中应保持金属丝的温度不变 |