关于向心力的下列说法中正确的是
| A.向心力不改变做圆周运动物体速度的大小 |
| B.做匀速圆周运动的物体,其向心力是不变的 |
| C.做圆周运动的物体,所受合力一定等于向心力 |
| D.做匀速圆周运动的物体,一定是所受的合外力充当向心力 |
如图所示,一小球用细绳悬挂于O点,将其拉离竖直位置一个角度后释放,则小球以O点为圆心做圆周运动,运动中小球所需的向心力是 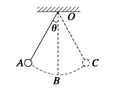
| A.绳的拉力 |
| B.重力和绳拉力的合力 |
| C.重力沿切线方向的分力 |
| D.绳的拉力和重力沿绳方向分力的合力 |
关于向心加速度,下列说法正确的是
| A.向心加速度是描述线速度变化的物理量 |
| B.向心加速度只改变线速度的方向,不改变线速度的大小 |
| C.向心加速度大小恒定,方向时刻改变 |
D.向心加速度的大小也可用a=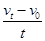 来计算 来计算 |
如图所示,质量为m的小球在竖直平面内的光滑圆环轨道上做圆周运动.圆环半径为R,小球经过圆环最高点时刚好不脱离圆环,则其通过最高点时( )
| A.小球对圆环的压力大小等于mg |
| B.小球受到的向心力等于0 |
C.小球的线速度大小等于 |
| D.小球的向心加速度大小等于g |
在竖直平面内有一个光滑的半圆轨道,轨道两端连线即直径在竖直方向,轨道半径为0.9m,一个质量为0.5kg的小球以一定的初速度滚上轨道(g=10m/s2)。求:
(1)小球在最高点不脱离轨道的最小速率是多少?
(2)小球在最高点速率v=4m/s时,小球对轨道的压力是多少?
(3)小球以v=4m/s的速率从最高点离开轨道,落地时的速度大小?速度方向与地面夹角的正切值?
如图所示,轻杆长1m,其两端各连接质量为1kg的小球,杆可绕距B端0.2m处的轴O在竖直面内转动,控制外部环境使A球转到最低点时速度大小为4m/s,此时B球的速度大小为 ,轴与杆之间的作用力大小为 。(g=10m/s2)
一个质量为m的物体(体积可忽略)在半径为R的光滑半球面顶点处以水平速度v0运动。如图所示,则下列结论中正确的是( )
| A.若v0 = 0,则物体对半球面顶点的压力大小等于mg |
B.若 ,则物体对半球面顶点无压力 ,则物体对半球面顶点无压力 |
C.若 ,则物体对半球面顶点的压力为 ,则物体对半球面顶点的压力为 |
D.若 则物体在半球面顶点下方的某个位置会离开半球面 则物体在半球面顶点下方的某个位置会离开半球面 |
如图所示,半径为r的圆筒,绕竖直中心轴 转动,小物块a靠在圆筒的内壁上,它与圆筒内壁的动摩擦因数为
转动,小物块a靠在圆筒的内壁上,它与圆筒内壁的动摩擦因数为 ,假设最大静摩擦力等于滑动摩擦力。要使a不下落,则圆筒转动的角速度至少为 ( )
,假设最大静摩擦力等于滑动摩擦力。要使a不下落,则圆筒转动的角速度至少为 ( )
A. |
B. |
C. |
D. |

甲、乙两个物体都做匀速圆周运动,转动半径比为3∶4,在相同的时间里甲转过60圈时,乙转过45圈,则它们的向心加速度之比为 ( )
| A.3:4 | B.4:3 | C.4:9 | D.9:16 |
如右图所示,A、B、C三个物体放在旋转平台上,动摩擦因数均为μ,已知A的质量为2m,B、C的质量均为m,A、B离轴距离均为R, C距离轴为2R,则当圆台旋转时
| A.C物体的向心加速度最大 |
| B.B物体的摩擦力最小 |
| C.当圆台转速增加时, A比C先滑动 |
| D.当圆台转速增加时, B比A先滑动 |
有一种杂技表演叫“飞车走壁”。由杂技演员驾驶摩托车沿圆台形表演台的侧壁,做匀速圆周运动。图中粗线圆表示摩托车的行驶轨迹,轨迹离地面的高度为h.下列说法中正确的是
| A.h越高,摩托车对侧壁的压力将越大 |
| B.h越高,摩托车做圆周运动的向心力将越大 |
| C.h越高,摩托车做圆周运动的周期将越小 |
| D.h越高,摩托车做圆周运动的线速度将越大 |
如图所示,一轻杆一端固定在O点,另一端固定一小球,在竖直平面内做圆周运动,通过最高点时,由于球对杆有作用,使杆发生了微小形变,关于杆的形变量与球在最高点时的速度大小关系,正确的是
| A.形变量越大,速度一定越大 | B.形变量越大,速度一定越小 |
| C.形变量为零,速度一定不为零 | D.速度为零,可能无形变 |
如图,地球赤道上的山丘e,近地资源卫星p和同步通信卫星q均在赤道平面上绕地心做匀速圆周运动。设e、p、q的圆周运动速率分别为v1、v2、v3,向心加速度分别为a1、 a2、a3,则
A.  |
B. |
C. |
D. |
一人用一根长L=1m,最大只能承受T=46N拉力的轻绳子,拴着一个质量m=1kg的小球(不考虑其大小),在竖直平面内作圆周运动,已知圆心O离地高H=21m,如图7所示,若小球运动到达最低点时绳刚好被球拉断,求
(1)小球到达最低点的速度大小是多少?
(2)小球落地点到O点的水平距离是多少?(g=10m/s2)
如图所示,在绕竖直轴匀速转动的水平圆盘盘面上,离轴心r = 20cm处放置一小物块A,其质量m = 2kg,试求:
(1)当圆盘转动的角速度ω = 2rad/s,转动一圈需要的时间是多少?物块A的速度是多少?
(2)A与盘面间的静摩擦力的最大值为其重力的0.5倍,若使A与盘面间不发生相对滑动,则圆盘转动的最大角速度是多大? (取g = 10m/s2)