要使单摆的振动周期变小,可采用下列哪些做法( )
| A.使摆球的质量减小 |
| B.使单摆的摆线变长 |
| C.将单摆从赤道移到北极 |
| D.将单摆从平原移到高山上 |
如图所示,一半径为R的圆弧形轨道固定在水平地面上,O为最低点,轨道末端A、B两点距离水平地面的高度分别为h和2h,h<<R。分别从A、B两点同时由静止释放甲、乙两个完全相同的小球。不计轨道与球之间的摩擦及空气阻力,不计两球碰撞过程中的机械能损失。则
A.碰撞后乙球经过 的时间再次回到点O
的时间再次回到点O
B.碰撞后乙球落到水平地面上时的速度大小为
C.碰撞后甲球落到水平地面上时的速度大小为
D.碰撞的瞬间前后相比较,轨道对地面的压力变小
某同学在做“利用单摆测重力加速度”的实验中,先测得摆线长为101.00cm,摆球直径为2.00cm,然后用秒表记录了单摆振动50次所用的时间为101.5 s。则:
(1)他测得的重力加速度g = m/s2.(计算结果取三位有效数字)
(2)他测得的g值偏小,可能原因是:
| A.实验中误将51次全振动计为50次。 |
| B.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了。 |
| C.开始计时时,秒表过迟按下。 |
| D.实验中误将49次全振动计为50次。 |
(3)为了提高实验精度,在实验中可改变几次摆长L并测出相应的周期T,从而得出一组对应的L和T的数值,再以L为横坐标、T2为纵坐标将所得数据连成直线,并求得该直线的斜率K。则重力加速度g = 。(用K表示)
对单摆的振动,以下说法中正确的是( )
| A.单摆摆动时,摆球受到的向心力大小处处相等 |
| B.摆球经过平衡位置时所受合外力为零 |
| C.摆球经过平衡位置时所受回复力为零 |
| D.单摆运动的回复力是摆球所受合力 |
一个单摆在质量为m1、半径为R1的星球上做周期为T1的简谐运动,在质量为m2、半径为R2的星球上做周期为T2的简谐运动,求T1与T2之比。
一个单摆在甲地时,在时间t内完成m次全振动,移至乙地时,经过相同的时间完成n次全振动,则甲、乙两地重力加速度大小之比g甲:g乙等于______________。
某同学在用单摆测定重力加速度的实验中,测量不同摆长情况下单摆的振动周期,并以L为横坐标, 为纵坐标,做出了
为纵坐标,做出了 图线,如图2所示,由此图线可知重力加速度为 。
图线,如图2所示,由此图线可知重力加速度为 。
如图2所示,是一个单摆(θ<10o),其周期为T,则下列正确的说法是( )
| A.把摆球的质量增加一倍,其周期变小 |
| B.把摆角变小时,则周期也变小 |
| C.此摆由O→B运动的时间为T/4 |
| D.摆球B→O时,动能向势能转化 |
如图所示,AB为半径R = 2m的一段光滑圆糟,A、B两点在同一水平高度上,且AB弧长10cm。将一小球从A点由静止开始释放,则它第一次运动到B点所用时间为( )
A. B.
B. C.π
C.π D.2π
D.2π
图(1)是利用砂摆演示简谐运动图象的装置。当盛砂的漏斗下面的薄木板被水平匀速拉出时,做简谐运动的漏斗漏出的砂在板上形成的曲线显示出砂摆的振动位移随时间变化的关系。第一次以速度v1匀速拉动木板,图(2)给出了砂摆振动的图线;第二次仅使砂摆的振幅减半,再以速度v2匀速拉动木板,图(3)给出了砂摆振动的图线。由此可知,砂摆两次振动的周期T1和T2以及拉动木板的速度v1和v2的关系是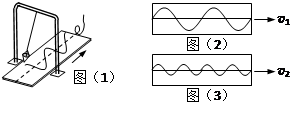
| A.T1∶T2=2∶1 | B.T1∶T2=1∶2 |
| C.v1∶v2=1∶2 | D.v1∶v2=2∶1 |
如图5所示是一个单摆在地球表面做受迫振动时的共振曲线,它表示振幅A与驱动力的频率f的关系,关于此单摆下列说法正确的是( )
| A.摆长约为10cm |
| B.摆长约为1m |
| C.若增大摆长,共振曲线的“峰”将向右移动 |
| D.若增大摆长,共振曲线的“峰”将向左移动 |
一个摆长为L1的单摆,在地面上做简谐运动,周期为T1,已知地球质量为M1,半径为R1,另一摆长为L2的单摆,在质量为M2,半径为R2的星球表面做简谐运动,周期为T2,若T1=2T2,L1=4L2,M1=4M2,则地球半径与星球半径之比R1∶R2为
| A.2∶1 | B.2∶3 |
| C.1∶2 | D.3∶2 |
如图所示,虚线和实线分别为甲、乙两个弹簧振子做简谐运动的图象.已知甲、乙两个振子质量相等,则
| A.甲、乙两振子的频率相同 |
| B.甲、乙两个振子的相位差恒为π |
| C.前2秒内甲、乙两振子的加速度均为正值 |
| D.第2秒末甲的速度最大,乙的加速度最大 |