如图所示的单摆,摆球a向右摆动到最低点时,恰好与一沿水平方向向左运动的黏性小球b发生碰撞,并黏接在一起,且摆动平面不变.已知碰撞前a球摆动的最高点与最低点的高度差为h,摆动的周期为T,a球质量是b球质量的5倍,碰撞前a球在最低点的速度是b球速度的一半.则碰撞后( )
A．摆动的周期为  T |
B．摆动的周期为  T |
| C．摆球的最高点与最低点的高度差为0.3 h |
| D．摆球的最高点与最低点的高度差为0.25 h |
一小球挂于O点，细线长为L，O点正下方L/2处有一铁钉。将小球拉至A处无初速释放，摆角很小，这个摆的周期是：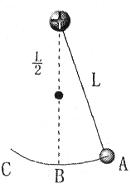
A． |
B． |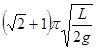
C． |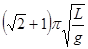
D． |
甲、乙两个单摆摆长相同，摆球质量之比为4：1．两个单摆在同一地点做简谐运动，摆球经过平衡位置时的速率之比为1：2，则两摆
| A．振幅相同，频率相同 | B．振幅不同，频率相同 |
| C．振幅相同，频率不同 | D．振幅不同，频率不同 |
甲、乙两个单摆摆长相同，摆球质量之比为4∶1，两个单摆在同一地点做简谐振动，摆球经过平衡位置时的速率之比为1∶2，则两摆 （ ）
| A．振幅相同，频率相同 | B．振幅不同，频率相同 |
| C．振幅相同，频率不同 | D．振幅不同，频率不同 |
利用传感器和计算机可以测量快速变化的力的瞬时值。右图是用这种方法获得的弹性绳中拉力随时间的变化图线。实验时，把小球举高到绳子的悬点O处，然后放手让小球自由下落。由此图线所提供的信息，以下判断正确的是 。
| A．t2时刻小球速度最大 |
| B．t1～t2期间小球速度先增大后减小 |
| C．t3时刻小球动能最小 |
| D．t1与t4时刻小球动量一定相同 |
做简谐振动的单摆摆长不变，把摆球质量增加为原来的4倍，使摆球经过平衡位置时的速度减小为原来的
倍，则单摆振动的
| A．周期、振幅都不变 | B．周期不变、振幅减小 |
| C．周期改变、振幅不变 | D．周期、振幅都改变 |
一单摆做小角度摆动，其振动图象如图，以下说法正确的是
| A．t1时刻摆球速度最大，悬线对它的拉力最小 |
| B．t2时刻摆球速度最大，振动方向沿x正方向 |
| C．t3时刻摆球速度为零，加速度最大，方向沿x负方向 |
| D．t4时刻摆球速度最大，悬线对它的拉力最大 |
有一摆长为L的单摆，悬点正下方某处有一小钉，当摆球经过平衡位置向左摆动时，摆线的上部将被小钉挡住，使摆长发生变化，现使摆球做小幅度摆动，摆球从右边最高点M至左边最高点N运动过程的闪光照片如右图所示，(悬点和小钉未被摄入)，P为摆动中的最低点。已知每相邻两次闪光的时间间隔相等，由此可知，小钉与悬点的距离为( )
| A．3L/4 | B．L/2 | C．L/4 | D．无法确定 |
如图所示，一单摆悬于O点，摆长为L，若在O点的竖直线上的O′点钉一个钉子，使OO′＝L/2，将单摆拉至A处释放，小球将在A、B、C间来回振动，若振动中摆线与竖直方向夹角小于10°，则此摆的周期是( )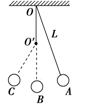
A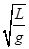．2π
B．2π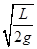
C．2π(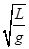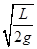＋ ) D．π(＋ )
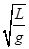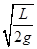做简谐振动的单摆摆长不变，若摆球质量增加为原来的4倍，摆球经过平衡位置时速度减小为原来的1/2，则单摆振动的( )
| A．频率、振幅都不变 | B．频率、振幅都改变 |
| C．频率不变，振幅改变 | D．频率改变，振幅不变 |
做简谐振动的单摆，在摆动的过程中( )
| A．只有在平衡位置时，回复力才等于重力和细绳拉力的合力 |
| B．只有在最高点时，回复力才等于重力和细绳拉力的合力 |
| C．小球在任意位置处，回复力都等于重力和细绳拉力的合力 |
| D．小球在任意位置处，回复力都不等于重力和细绳拉力的合力 |
要使单摆的振动周期变小，可采用下列哪些做法( )
| A．使摆球的质量减小 |
| B．使单摆的摆线变长 |
| C．将单摆从赤道移到北极 |
| D．将单摆从平原移到高山上 |
如图所示，一半径为R的圆弧形轨道固定在水平地面上，O为最低点，轨道末端A、B两点距离水平地面的高度分别为h和2h，h<<R。分别从A、B两点同时由静止释放甲、乙两个完全相同的小球。不计轨道与球之间的摩擦及空气阻力，不计两球碰撞过程中的机械能损失。则
A．碰撞后乙球经过
的时间再次回到点O
B．碰撞后乙球落到水平地面上时的速度大小为
C．碰撞后甲球落到水平地面上时的速度大小为
D．碰撞的瞬间前后相比较，轨道对地面的压力变小
粤公网安备 44130202000953号