做简谐振动的单摆摆长不变，若摆球质量增加为原来的4倍，摆球经过平衡位置时速度减小为原来的1/2，则单摆振动的（ ）
| A．频率、振幅都不变 | B．频率、振幅都改变 |
| C．频率不变，振幅改变 | D．频率改变，振幅不变 |
振动着的单摆摆球通过平衡位置时，它受到的回复力（ ）
| A．指向地面 | B．指向悬点 |
| C．为零 | D．垂直摆线，指向运动方向 |
有一摆长为L的单摆，悬点正下方某处有一小钉，当摆球经过平衡位置向左摆动时，摆线的上部将被挡住，使摆长发生变化。现使摆球做小幅度摆动，摆球从右边最高点M至左边最高点N的一次全过程的闪光照片，如图所示（悬点和小钉未被摄入）。P为摆动中的最低点，已知每相邻两次闪光的时间间隔相等，由此可知，小钉与悬点的距离为 （ ）
| A．L/4 | B．L/2 | C．3L/4 | D．无法确定 |
做简谐运动的单摆摆长不变，若摆球质量增加为原来的4倍，摆球经过平衡位置时速度减小为原来的1／2，则单摆振动的
| A．频率、振幅都不变 | B．频率不变、振幅改变 |
| C．频率、振幅都改变 | D．频率改变、振幅不变 |
如图所示为一单摆．O为平衡位置，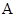
、
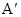分别是左右两个位移的最大位置，且摆角
．则下列说法中正确的是（ ）
| A．小球从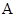→O的过程中，由小球受到的重力和细线的拉力的合力来提供回复力 |
| B．小球每次经过平衡位置O时，小球的动能和动量、回复力均相同 |
| C．小球从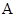→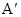的过程中，小球的加速度先增大后减小，速度先减小后增大 |
D．如果这个单摆在质量为M、半径为R的地球表面上做简谐运动时的周期为T，那么，这个单摆在质量为m、半径为r的月球表面上做简谐运动的周期为 |
在做“用单摆测定重力加速度”的实验中，有人提出以下几点建议，其中对提高测量结果精度有利的是 （ ）
| A．适当加长摆线 |
| B．质量相同、体积不同的摆球，应选用体积较大的 |
| C．单摆偏离平衡位置的角度不能太大 |
| D．当单摆经过平衡位置时开始计时，经过一次全振动后停止计时，用此时间间隔作为单摆振动的周期 |
单摆做简谐运动时，其回复力是 （ ）
| A．摆球所受的重力 | B．悬线对摆球的拉力 |
| C．摆球重力在垂直悬线方向上的分力 | D．摆球所受重力与悬线拉力的合力 |
如图甲所示为一简谐波在t=0时刻的图象，图乙所示为x=4m处的质点P的振
动图象，则下列判断正确的是 （ ）
| A．这列波的波速是2m/s |
| B．这列波的传播方向沿x正方向 |
| C．t=3．5s时P点的位移为0．2m |
D．从t=0时刻开始P点的振动方程为 m |
如图7所示，光滑槽的半径R远大于小球运动的弧长，今有两个小球(视为质点)同时由静止释放，其中甲球开始时离圆槽最低点O较远些，则它们第一次相遇的地点是在( )
| A．O点 | B．O点偏左 |
| C．O点偏右 | D．无法确定，因为两小球的质量关系未知 |
一个打磨得很光滑的凹镜，其曲面半径远大于曲面长度，将镜面水平放置，如图所示。现让一个小球（小球可视为质点）从镜边缘静止释放，小球在镜面上将作往复运动，以下说法中正确的是（ ）
| A．小球质量越大，往复运动的周期越长 |
| B．释放点离最低点距离越大，周期越短 |
| C．凹镜曲面半径越大，周期越长 |
| D．周期应由小球质量、释放点离平衡位置的距离，以及曲面半径共同决定 |
图3中各摆球可视为质点，各段绳长均为l，摆角均小于10°，(a)图在垂直纸面内摆动，(b)图中电梯匀加速上升，加速度为a，(c)图摆球带正电，磁场垂直纸面向外，(d)图摆球带正电，电场方向向下．以下说法正确的是（ ）
| A．a图中摆球的周期最小 | B．b和d图中摆球的周期不可能相等 |
| C．c图中摆球的周期与未加磁场时是相同的 | D．d图中摆球的周期是最大的 |
用单摆测重力加速度的实验中，用的摆球密度不均匀，无法确定重心位置。第一次量得悬线长L1，测得周期为T1；第二次测得悬线长为L2，周期为T2，根据上述数据，g值应为
A． |
B． |
C． |
D．无法确定 |
如果他测得的g值偏小，可能的原因是
| A．测摆线长时摆线拉得过紧 |
| B．摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了 |
| C．开始计时，秒表过迟按下 |
| D．实验中误将49次全振动数为50次 |
做简谐运动的单摆摆长不变，若摆球质量增加为原来的4倍，摆球经过平衡位置时速度减小为原来的1／2，则单摆振动的
| A．频率、振幅都不变 | B．频率不变、振幅改变 |
| C．频率、振幅都改变 | D．频率改变、振幅不变 |
粤公网安备 44130202000953号