高中物理验证牛顿第二运动定律计算题

如图所示，在一光滑水平的桌面上，放置一质量为M．宽为L的足够长“U”形框架，其ab部分电阻为R，框架其他部分的电阻不计．垂直框架两边放一质量为m．电阻为R的金属棒cd，它们之间的动摩擦因数为μ，棒通过细线跨过一定滑轮与劲度系数为k．另一端固定的轻弹簧相连．开始弹簧处于自然状态，框架和棒均静止．现在让框架在大小为2 μmg的水平拉力作用下，向右做加速运动，引起棒的运动可看成是缓慢的．水平桌面位于竖直向上的匀强磁场中，磁感应强度为B．问：
(1)框架和棒刚开始运动的瞬间，框架的加速度为多大?
(2)框架最后做匀速运动(棒处于静止状态)时的速度多大?
(3)若框架通过位移s后开始匀速运动，已知弹簧弹性势能的表达式为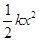(x为弹簧的形变量)，则在框架通过位移s的过程中，回路中产生的电热为多少?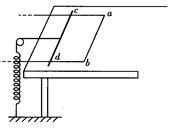

如图所示，以A、B和C、D为断点的两半圆形光滑轨道固定于竖直平面内，一滑板静止在光滑的地面上，左端紧靠B点，上表面所在平面与两半圆分别相切于B、C两点，一物块（视为质点）被轻放在水平匀速运动的传送带上E点，运动到A点时刚好与传送带速度相同，然后经A点沿半圆轨道滑下，再经B点滑上滑板，滑板运动到C点时被牢固粘连。物块可视为质点，质量为m,滑板质量为M=2m，两半圆半径均为R,板长l=6.5R,板右端到C点的距离L在R<L<5R范围内取值，E点距A点的距离s=5R，物块与传送带、物块与滑板间的动摩擦因数均为，重力加速度g已知。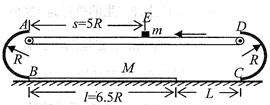

(1)求物块滑到B点的速度大小;
(2)求物块滑到B点时所受半圆轨道的支持力的大小;
(3)试讨论物块从滑上滑板到离开右端的过程中，克服摩擦力做的功与L的关系;并判断物块能否滑到CD轨道的中点。