在“探究弹力与弹簧伸长的关系”的实验中。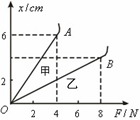
①关于操作步骤先后顺序，下列说法正确的是
A．先测量原长，后竖直悬挂
B．先竖直悬挂，后测量原长
C．先后顺序对实验结果无影响
D．先后顺序对实验结果的影响程度取决于弹簧的自重
②为了探求弹簧弹力F和弹簧伸长量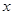
的关系，李强同学选了甲、乙两根规格不同的弹簧进行测试，根据测得的数据绘出如图所示的图象，从图象上看，该同学没能完全按实验要求做，使图象上端成为曲线，图象上端成为曲线是因为 .这两根弹簧的劲度系数分别为：甲弹簧为 N/m，乙弹簧为
N/m。若要制作一个精确度较高的弹簧秤，应选弹簧 (填“甲”或“乙”)。
③以下是一位同学准备完成的实验步骤，请你帮这位同学按操作的先后顺序，用字母排列出来是： .
A．以弹簧伸长量为横坐标，以弹力为纵坐标，描出各组数据（x，F）对应的点，并用平滑的曲线连结起来.
B．记下弹簧不挂钩码时，其下端在刻度尺上的刻度L0
C．将铁架台固定于桌子上，并将弹簧的一端系于横梁上，在弹簧附近竖直固定一刻度尺
D．依次在弹簧下端挂上1个、2个、3个、4个……钩码，并分别记下钩码静止时，弹簧下端所对应的刻度并记录在表格内，然后取下钩码
E．以弹簧伸长量为自变量，写出弹力与弹簧伸长量的关系式。
F．解释函数表达式中常数的物理意义。
④下表是这位同学探究弹力大小与弹簧伸长量之间的关系所测的几组数据：
| 弹力（F/N） |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
| 弹簧原来长度（L0/cm） |
15 |
15 |
15 |
15 |
15 |
| 弹簧后来长度（L/cm） |
16.2 |
17.3 |
18.5 |
19.6 |
20.8 |
| 弹簧伸长量（x/cm） |
|
|
|
|
|
请你算出每一次弹簧伸长量，并将结果填在上表的空格内；在图11的坐标上作出F-x图线；并写出曲线的函数表达式（x用cm作单位）： ，其中常数的物理意义表示：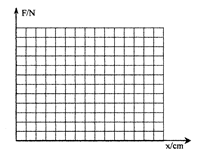 
在《探究求合力的方法》的实验中，下列说法正确的是 （ ）
| A．用三个已校好的弹簧秤才能完成此实验 |
| B．用两个已校好的弹簧秤就可以完成此实验 |
| C．用一个已校好的弹簧秤也能完成此实验、 |
| D．实验中弹簧秤的外壳与纸面间的摩擦将会影响实验的结果 |
（1）某同学在做“利用单摆测重力加速度”的实验时，有下列步骤，其中正确的是
（不定项）
A．取长度约1m的细线，一端固定在铁架台上，另一端栓一个小铁球
B．测出细线的长度即为单摆的摆长L
C．使小铁球离开其平衡位置约30cm的距离，将其静止释放
D．待小铁球摆动稳定后，当小铁球经过平衡位置时按下秒表开始计时
E．开始计时时记为1，当小铁球第50次经过平衡位置停止计时，所测时间为50个周期（t=50T）
（2）若某次测量时间结果如图所示，则秒表的读数是
（3）若测出的g值较当地重力加速度的值偏大，可能原因是 （不定项）
A．小球的质量偏大
B．用摆线的长度当作摆长
C．将实际振动n次数误记为（n+1）次
D．摆线上端没有系牢，摆动过程因松动而使摆线变长 s。
如图为用单摆测重力加速度的实验
（1）（多选题）为了减小误差，下列措施正确的是
| A．摆线长度L应为线长与摆球半径的和，且在20 cm左右 |
| B．在摆线上端的悬点处，用开有夹缝的橡皮塞夹牢摆线 |
| C．在铁架台的竖直杆上固定一个标志物，且尽量使标志物靠近摆线 |
| D．计时起终点都应在摆球的最高点且不少于30次全振动的时间 |
（2）某同学正确操作，得到了摆长L和 n次全振动的时间t，由此可知这个单摆的周期T=________；当地的重力加速度g=____________。
某兴趣小组为了测一遥控电动小车的功率，进行了如下实验：
（1）用天平测出小车的质量为0.4 kg；（2）正确地将电动小车、纸带和打点计时器安装好；（3）接通打点计时器（其打点时间间隔为0.02 s）；（4）使小车加速运动，达到最大速度一段时间后关闭小车电源，待小车静止时再关闭打点计时器（设电动小车的功率恒定，在运动过程中小车所受阻力恒定不变）在上述过程中，打点计时器在纸带上打下的部分点 迹如图所示，请你分析纸带数据，并将结果填写在下列空格中：（保留两位有效数字）
（1）该电动小车运动的最大速度为_________m/s；
（2）该电动小车的功率为_________W。 
某同学在“用打点计时器测速度”的实验中，用打点计时器记录了被小车拖动的纸带的运动情况，在纸带上确定出0、1、2、3、4、5、6共7个测量点。其相邻点间的距离如图所示，每两个相邻的测量点之间的时间间隔为
，完成下面问题。
(1)根据打点计时器打出的纸带，我们可以直接得到的物理量是
| A．时间间隔 | B．加速度 |
| C．瞬时速度 | D．平均速度 |
（2）根据纸带上各个测量点间的距离，某同学已将1、2、3、5点对应的时刻的瞬时速度进行计算
并填入表中，请你将4点对应的时刻的瞬时速度填入表中；（要求保留3位有效数字）
| 瞬时速度 |
v1 |
v2 |
v3 |
v4 |
v5 |
| 数值(m/s) |
0.165 |
0.214 |
0.263 |
|
0.363 |
（3）在图所示的直角坐标系中画出小车的瞬时速度随时间变化的关系图线。
（4）由图像求出小车的加速度
（1）在利用单摆测定重力加速度的实验中，若测得的g值偏大，可能的原因是（ ）
A．摆球质量过大
B．单摆振动时振幅较小
C．测量摆长时，只考虑了线长，忽略了小球的半径
D．测量周期时，把n个全振动误认为（n+1）个全振动，使周期偏小
（2）在演示简谐运动图象的沙摆实验中，使木板沿直线OO′做匀加速直线运动，摆动着的漏斗中漏出的沙在木板上显示出如图乙所示曲线，A．B．C．D均为直线OO′上的点，测出
="16" cm,
="48" cm，摆长为64 cm（可视为不变），摆角小于5°，则该沙摆的周期为______s，木板的加速度大小约为_____
_ m/s2（g取10m/s2）
“验证力的平行四边形定则”实验中
（1）部分实验步骤如下，请完成有关内容：
A．将一根橡皮筋的一端固定在贴有白纸的竖直平整木板上，另一端绑上两根细线．
B．在其中一根细线挂上5个质量相等的钩码，使橡皮筋拉伸，如图(1)所示，记录： 、 、 ．
C．将步骤B中的钩码取下，分别在两根细线上挂上4个和3个质量相等的钩码，用两
光滑硬棒B、C使两细线互成角度，如图(2)所示，小心调整B、C的位置，使 ，记录 ．
（2）如果“力的平行四边形定则”得到验证，那么图(2)中
= ．
如图6-1-14是以左心室为例，一个成年人在一次血液循环中左心室容积和压力变化的p—V曲线，成年人正常心跳每分钟约75次，左右心室收缩时射出的血量约为70ml，右心室对肺动脉的压力约为左心室的1／5，则可估算出心脏工作的平均功率约为 
在绳的上、下两端各拴着一小球，一人用手拿住绳上端的小球站在三层楼的阳台上，放手后小球自由下落，两小球落地的时间差为
，如果人站在四层楼的阳台上，放手让其自由下落，两小球落地的时间差将（空气阻力不计）________ （填“增大”、“减小”、“不变”）．[1]
竖直上抛的物体，在上升阶段的平均速度是20 m/s，则从抛出到落回抛出点所需时间为______s，上升的最大高度为_______m．（g=10m/s2）[2]
图2-3（原图2-8）是在高速公路上用超声波测速仪测量车速的示意图，测速仪发出并接收超声波脉冲信号。根据发出和接收到的信号间的时间差，测出被测物体的速度。图2-4（原图2-9）中p1、p2是测速仪发出的超声波信号，n1、n2分别是p1、p2由汽车反射回来的信号．设测速仪匀速扫描，p1、p2之间的时间间隔△t = 1.0s，超声波在空气中传播的速度是v = 340m/s，若汽车是匀速运动的，则根据图2-9可知，汽车在接收到p1、p2两个信号之间的时间内前进的距离是__________m，汽车的速度是___________m/s． [8]
天文观测表明，几乎所有远处的恒星（或星系）都以各自的速度背离我们而运动，离我们越远的星体，背离我们运动的速度（称为退行速度）越大；也就是说，宇宙在膨胀．不同星体的退行速度v和它们离我们的距离r成正比，即
v = Hr
式中H为一常量，已由天文观察测定．为解释上述现象，有人提出一种理论，认为宇宙是从一个大爆炸的火球开始形成的．假设大爆炸后各星体以不同的速度向外匀速运动，并设想我们就位于其中心，则速度大的星体现在离我们越远．这一结果与上述天文观测一致．
由上述理论和天文观测结果，可估算宇宙年龄T，其计算式为T ____________．根据过去观测，哈勃常数H = 3×10－2m/s·l.y.，其中l.y.(光年)是光在1a(年)中行进的距离，由此估算宇宙的年龄约为__________________a．（1999年．上海卷）[6]
一物体由静止开始沿直线运动，其加速度随时间变化的图像如图2－4所示，若从出发开始计时，则4s秒末物体离开出发点 m，此时物体的瞬时速度为 ．
粤公网安备 44130202000953号