“验证机械能守恒定律”的实验采用重物自由下落的方法.
(1)用公式mgh= mv2时,对纸带上起点的要求是____________,为此目的,所选择的纸带一、二两点间距应接近_______________.
mv2时,对纸带上起点的要求是____________,为此目的,所选择的纸带一、二两点间距应接近_______________.
(2)若实验中所用的重锤质量m=1kg,打点纸带如图所示,打点时间间隔为0.02s,则记录B点时,重锤的速度vB=__________,重锤动能EkB=___________.从开始下落起至B点,重锤的重力势能减少量是____________,因此可得出的结论是___________.
如图7-7-9所示,轻弹簧k一端与墙相连,质量为4 kg的木块沿光滑的水平面以5 m/s的速度运动并压缩弹簧k,求弹簧在被压缩过程中最大的弹性势能及木块的速度减为3 m/s时弹簧的弹性势能.
图7-7-9
一根弹簧的左端固定在墙上,如图7-7-8所示.一个质量为m、速度为v0的物体在光滑水平地面上向左滑行,压缩弹簧,这时m的动能将___________,弹簧的弹性势能将___________,物体m与弹簧组成的系统的机械能将___________,弹簧的最大压缩弹性势能是___________.
图7-7-8
如图7-7-2所示,一个质量为m的物体自高h处自由下落,落在一个劲度系数为k的轻质弹簧上.求:当物体速度达到最大值v时,弹簧对物体做的功为多少?
图7-7-2
如图所示,在光滑水平面上有一质量为M的小车,小车与绳子的一端相连,绳子的另一端通过不计摩擦的滑轮吊一个质量为m的砝码,砝码离地高h.若把小车从静止开始释放,则当砝码着地时小车的速度为__________,在此过程中,绳子拉力对小车所做的功为____________(此过程中M没有碰到滑轮).
如图所示,小球从光滑斜面上无初速度滚下,然后进入光滑圆轨道的内侧,在轨道中做圆周运动.已知圆轨道的半径为r,要使小球能在圆轨道内做完整的圆周运动,小球应至少在多高的地方释放?
质量为m、摆长为L的摆球从摆角为53°处无初速地摆下,不计空气阻力,设摆球在最低点处的重力势能为零,那么当摆球的摆角θ=________时,摆球的动能和重力势能相等.(sin53°=0.8)
 某实验小组利用如图甲所示的实验装置来验证钩码和滑块所组成的系统机械能守恒.
某实验小组利用如图甲所示的实验装置来验证钩码和滑块所组成的系统机械能守恒.
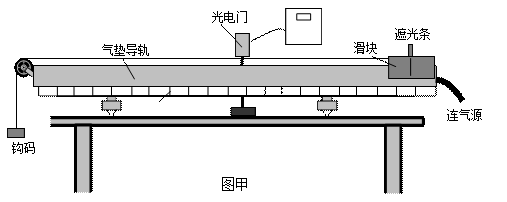

(1)实验前需要调整气垫导轨底座使之水平,利用现有器材如何判断导轨是否水平?
.
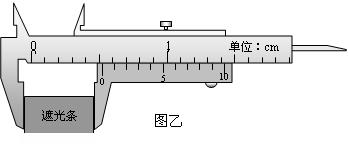
(2)如图乙所示,用游标卡尺测得遮光条的宽度d= cm;实验时将滑块从图示位置由静止释放,由数字计时器读出遮光条通过光电门的时间Δt=1.2×10-2s,则滑块经过光电门时的瞬时速度为 m/s.在本次实验中还需要测量的物理量有:钩码的质量m、 和 (文字说明并用相应的字母表示).
(3)本实验通过比较 和 在实验误差允许的范围内相等(用测量的物理量符号表示),从而验证了系统的机械能守恒.