高中物理原子的核式结构计算题

【物理－物理3-5】
（1）置于铅盒中的放射源发射的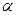、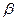和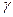三种射线，由铅盒的小孔射出，在小孔外放一张铝箔，铝箔后的空间有一匀强电场。射线进入电场后，变为a、b两束，射线a沿原来方向行进，射线b发生了偏转，如图所示，则图中的射线a为_________射线，射线b为___________射线。

（2）如图所示，平放在水平面上的轻质弹簧的一端固定在竖直墙上，质量为 的光滑弧形槽静止在光滑水平面上，底部与水平面平滑连接。一个质量为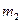的小球从槽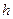高处由静止开始下滑，要使小球能与弧形槽发生第二次作用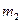，、应满足怎样的条件？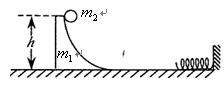

模块3-5试题
（I）        首先提示了原子具有复杂的结构，     首先揭示了原子核具有复杂的结构。

A．电子的发现	B．质子的发现
C．中子的发现	D．天然放射现象的发现

（II）介子由两个夸克构成，而夸克之间的相互作用相当复杂。研究介子可通过用高能电子与其发生弹性碰撞来进行。由于碰撞过程难于分析，为掌握其主要内涵，人们假设了一种简化了的“分粒子”模型。其主要内容为：电子只和介子的某部分（比如其中一个夸克）做弹性碰撞。碰撞后的夸克再经过介子内的相互作用把能量和动量传给整个介子。“分粒子”模型可用下面的简化模型来阐述：一个电子质量为m₁，动能为E₀，与介子的一个夸克（质量为m₂）做弹性碰撞。介子里另一个夸克的质量为m₃，夸克间以一根无质量的弹簧相连。碰撞前夸克处于静止状态，弹簧处于自然长度。试求：
（1）夸克m₂与电子碰撞后所获得的动能
（2）介子作为一个整体所具有的以弹簧弹性势能形式代表的介子的最大内能。

静止在匀强磁场中的放射性原子核X发生衰变，衰变后带电粒子运动速度和磁感线垂直，两轨迹圆半径之比，带电粒子在轨迹圆上运动的周期之比。设衰变过程释放的核能全部转化成射线粒子和反冲核的动能，已知该衰变过程前后原子核的质量亏损为m。
(1)该衰变为          衰变。(填“”或“”)
(2)写出核反应方程(反冲核的元素符号可用Y表示)：          。
(3)计算射线粒子和反冲核的动能。

（1）下列说法正确的是（选对一个给2分，选对两个给4分，选对三个给6分，选错一个扣3分，最低得分为0分）

A．卢瑟福通过粒子散射实验，提出了原子的核式结构模型

B．在很多核反应中，由于有核能的释放，所以才会有质量的亏损

C．对放射性物质施加压力，其半衰期将减少

D．入射光的频率如果低于某金属的截止频率，即使增加该入射光的强度，也不能使该金属发生光电效应

E．康普顿效应不仅表明了光子具有能量，还表明了光子具有动量
（2）如图所示为氢原子的能级图，n为量子数。在氢原子核外电子由量子数为 2的轨道跃迁到量子数为3的轨道的过程中，将     （填“吸收”、“放出”）光子。若该光子恰能使某金属产生光电效应，则一群处于量子数为4的激发态的氢原子在向基态跃迁的过程中，有     种频率的光子能使该金属产生光电效应。

（3）（9分) 如图所示，一质量m₁= 0.48kg的平板小车静止在光滑的水平轨道上。车顶右端放一质量m₂= 0.2kg的小物块，小物块可视为质点。现有一质量m₀= 0.02kg的子弹以水平速度射中小车左端，并留在车中，最终小物块以5m/s的速度与小车脱离。子弹与车相互作用时间极短。g取10 m/s²。求：

① 子弹刚刚射入小车时，小车速度v₁的大小；
② 小物块脱离小车时，小车速度v₁′的大小。

下列说法中正确的是(    )

A．一般物体辐射电磁波的情况与物体的温度、物体的材料有关

B．对于同一种金属来说，其极限频率恒定，与入射光的频率及光的强度均无关

C．汤姆孙发现电子，表明原子具有核式结构

D．E=mc^2表明物体具有的能量与其质量成正比

E．“人造太阳”的核反应方程是

一速度为v的高速α粒子（）与同方向运动的氖核（）发生弹性正碰，碰后α粒子恰好静止。求碰撞前后氖核的速度（不计相对论修正）。

已知镭的原子序数是88，原子核质量数是226。试问：
①镭核中有几个质子？几个中子？
②镭核所带电荷量为多少？
③若镭原子呈中性，它核外有几个电子？
④是镭的一种同位素，让226 88R_a和228 88R_a以相同速度垂直射入磁应强度为B的匀强磁场中，它们运动的轨道半径之比是多少？

（本题6分）已知镭的原子序数是88，原子核质量数是226.试问：
（1）镭核中有几个质子？几个中子？
(2)镭核所带的电荷量是多少？
（3）呈中性的镭原子，核外有几个电子？

设原子核的电荷量为Q，电子的电荷量为e，静电力常量为k，核外有一个电子在距核为r的轨道上绕核旋转.求此电子的动能.

天文学家测得银河系中氦的含量约为25%.有关研究表明,宇宙中氦生成的途径有两条:一是在宇宙诞生后3分钟左右生成的;二是在宇宙演化到恒星诞生后,由恒星内的氢核聚变反应生成的.
(1)把氢核聚变反应简化为4个氢核()聚变成氦核(),同时放出2个正电子()和2个中微子(ν₀),请写出该氢核聚变反应的方程,并计算一次反应释放的能量.
(2)研究表明,银河系的年龄约为t=3.8×10¹⁷ s,每秒钟银河系产生的能量约为1×10³⁷ J(即P=1×10³⁷ J/s).现假定该能量全部来自上述氢核聚变反应,试估算银河系中氦的含量(最后结果保留一位有效数字).
(3)根据你的估算结果,对银河系中氦的主要生成途径作出判断.
(可能用到的数据:银河系质量约为M=3×10⁴¹ kg,原子质量单位1 u=1.66×10^-27 kg,1 u 相当于1.5×10^-10 J的能量,电子质量m_e="0.000" 5 u,氦核质量m_α="4.002" 6 u,氢核质量m_p="1.007" 8 u,中微子ν_e质量为零)