高中物理信息传播、处理和存储技术的发展计算题

如图所示，一根长直棒AB竖直地插入水平池底，水深a=0.8m，棒露出水面部分的长度b=0.6m，太阳光斜射到水面上，与水面夹角 =37°，已知水的折射率n= ，sin37°=0.6，cos37°=0.8．求：

①太阳光射入水中的折射角β；
②棒在池底的影长l．

如图所示，直角玻璃三棱镜置于空气中，∠A＝60°，∠C＝90°，一束极细的光于AC边的中点D垂直AC面入射，已知AD＝a，棱镜的折射率n＝，光在真空中的传播速度为c。求：
（ⅰ）光从棱镜第一次射入空气时的折射角；
（ⅱ）光从进入棱镜到它第一次射入空气所经历的时间（结果可以用根式表示）。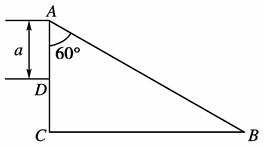

(6分)光纤通信是70年代以后发展起来的新兴技术，世界上许多国家都在积极研究和发展这种技术．发射导弹时，可在导弹后面连一根细如蛛丝的光纤，就像放风筝一样，这种纤细的光纤在导弹和发射装置之间，起着双向传输信号的作用．光纤制导的下行光信号是镓铝砷激光器发出的在纤芯中波长为0.85的单色光．上行光信号是铟镓砷磷发光二极管发射的在纤芯中波长为1.06的单色光．这样操纵系统通过这根光纤向导弹发出控制指令，导弹就如同长“眼睛”一样盯住目标．根据以上信息，回答下列问题：
①在光纤制导中，上行光信号在真空中波长是多少？
②为什么上行光信号和下行光信号要采用两种不同频率的光？(已知光纤纤芯的折射率为1.47)

折射率为n、长度为L的玻璃纤维置于空气中，若从A端射入的光线能在玻璃纤维中发生全反射，最后从B端射出，如图所示，求：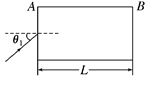

①光在A面上入射角的最大值．
②若光在纤维中恰能发生全反射，由A端射入到从B端射出经历的时间是多少？

一位学生用如图所示的方法来测定水的折射率，该学生在一个游泳池测得池中水深h="1.2" m（池底水平），用一根竹竿竖直立于池底，浸入水中部分刚好是全长的一半，太阳光与水平方向成θ=37°角射入游泳池，池底竹竿顶端的影子到竹竿底端的距离为L="2.5" m，求水的折射率和光在水中的传播速度。（sin37°=0.6，cos37°=0.8）

晴天的晚上,人能看见卫星的条件是卫星被太阳照着且在人的视野之内.一个可看成漫反射体的人造地球卫星的圆形轨道与赤道共面,卫星自西向东运动.春分期间太阳垂直射向赤道,赤道上某处的人在日落后8 h时在西边的地平线附近恰能看到它,之后极快地变暗而看不到了.已知地球的半径R_地=6.4×10⁶ m,地面上的重力加速度为10 m/s²,估算:(答案要求精确到两位有效数字)
(1)卫星轨道离地面的高度;
(2)卫星的速度大小.

宽度为d的平面镜MN立于水平地面上,在平面镜的正前方的A点处(A点到平面镜的两端点M､N的距离相等),有一人面对平面镜站在水平地面上,A点距离镜面h远,在平面镜的前方与镜面平行的直线PQ上有一点光源S,从远处以速度v沿直线QP运动,如图所示,已知PQ到平面镜MN所在直线的距离为H,且H>h.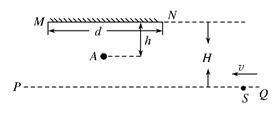

(1)点光源S沿QP直线运动,在某一个范围内可以被A点的人通过平面镜看到,请用作图法画出人通过平面镜可看到发光点S的范围,在图中用斜线表示出来;
(2)人通过平面镜可以看到发光点S的时间是多少?

如图所示,点光源S位于光屏AB的右方,平面镜MN初始时与光屏AB平行,点光源S发出的光从光屏AB上的小孔P射到平面镜上的O点,SO⊥MN,PO=d,今将平面镜绕着过O点的轴逆时针方向匀速转动,角速度为ω.求:

(1)从初始位置开始转过30°角的过程中,光线SO经平面镜反射落在光屏AB上的斑点Q移动的平均速度;
(2)平面镜转到与初始位置夹30°角的瞬间,斑点在光屏上移动的瞬时速度.

如图所示，一束光线以60°的入射角射到一水平放置的平面镜上，反射后在上方与平面镜平行的光屏上留下一光点P，现在将一块上下两面平行的透明体平放在平面镜上，则进入透明体的光线经平面镜反射后再从透明体的上表面射出，打在光屏上的P′点，与原来相比向左平移了3.46 cm，已知透明体对光的折射率为.求光在透明体里运动的时间．