某时刻的波形图如图所示,波沿x轴正方向传播,质点P的横坐标x=0.32m.从此时刻开始计时
若P点经0.4s第一次到达最大正位移处,求波速大小.
若P点经0.4s到达平衡位置,波速大小又如何?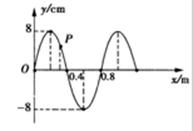
如图所示,沿波的传播方向上有间距均为2m的五个质点,均静止在各自的平衡位置,一列简谐横波以2m/s的速度水平向右传播,t=0时刻到达质点a,质点a开始由平衡位置向下运动,t=3s时质点a第一次到达最高点,在下列说法中正确的是( ) (选对一个给3分,选对两个给4分,选对三个给6分。每选错一个扣3分,最低得分为0分)
| A.质点d开始振动后的振动周期为4s |
| B.t=4s时刻波恰好传到质点e |
| C.t=5s时刻质点b到达最高点 |
| D.在3s<t<4s这段时间内质点c速度方向向上 |
E. 这列简谐横波的波长为4m
P、Q是一列简谐横波中的两质点,已知P离振源较近,P、Q两点的平衡位置相距15m(小于一个波长),各自的振动图象如图所示。此列波的波速为 m/s。
一列简谐横波沿直线由a向b传播,相距21m的a、b两处的质点振动图象如图中a、b所示,则
| A.该波的振幅是20cm | B.该波的波长可能是12m |
| C.该波的波速可能是10 m/s | D.该波由a传播到b最短历时3.5 |
一列沿x轴传播的简谐横波在某时刻波的图象如图所示,已知波速为20 m/s,图示时刻x=2.0m处的质点振动速度方向沿y轴负方向,可以判断
| A.质点振动的周期为0.20s |
| B.质点振动的振幅为1.6cm |
| C.波沿x轴的正方向传播 |
| D.图示时刻,x=1.5m处的质点加速度沿y轴正方向 |
一列简谐横波在x轴上传播,在t1=0和t2=0.05s时刻,其波形图分别如图中的实线和虚线所示,求: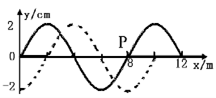
(1)该波的振幅和波长?
(2)若这列波向右传播,波速是多少?若这列波向左传播,波速是多少?
A、B两列简谐横波均沿x轴正向传播,在某时刻的波形分别如图甲、乙所示,经过时间t(t小于A波的周期TA),这两列简谐横波的波形分别变为图丙、丁所示,则A、B两列波的波速vA、vB之比不可能的是:( )
A.1∶1 B.1∶2 C.1∶3 D.3∶1
有关电磁场和电磁波,下列说法中正确的是:( )
| A.麦克斯韦首先预言并证明了电磁波的存在 |
| B.变化的电场一定产生变化的磁场 |
| C.使用空间波来传播信息时主要是应用无线电波波长大、衍射现象明显,该可以绕过地面上的障碍物 |
| D.频率为750KHz的电磁波在真空中传播时,其波长为400m |
如图所示,在x轴上传播的一列简谐横波,实线表示t=0时刻的波形图,虚线表示在t=0.2s时刻的波形图。已知该波的波速是80m/s,则下列说法正确的是
| A.波长是10m |
| B.周期是0.1s |
| C.波可能沿x轴正方向传播 |
| D.t=0时,x=4m处的质点速度沿y轴负方向 |
一列声波从空气传入水中,已知水中声速较大,则
| A.声波频率不变,波长变小 | B.声波频率不变,波长变大 |
| C.声波频率变小,波长变大 | D.声波频率变大,波长不变 |
如图所示,是一列沿着x轴正方向传播的横波在t=0时刻的波形图,已知这列波的周期T=2.0s。下列说法正确的是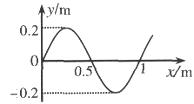
| A.这列波的波速v="2.0" m/s |
| B.在t=0时,x=0.5m处的质点速度为零 |
| C.经过2.0s,这列波沿x轴正方向传播0.8m |
| D.在t=0.3s时,x=0.5m处的质点的运动方向为y轴正方向 |
如图所示,一列简谐横波沿x轴传播,实线为t1=0时的波形图,此时P质点向y轴负方向运动,虚线为t2=0.1s时的波形图。已知t2-t1<T,T为波的周期。求:
(1)波的传播方向和波长λ;
(2)这列波的传播速度;
(3)这列波的频率。
如图所示,图中的实线是一列简谐横波在某一时刻的波形图。经过0.5s后,其波形图如图中虚线所示。
(1)如果波是沿x轴正方向传播的,且周期T > 0.5s,则波的速度为_________m/s;
(2)如果波是沿x轴负方向传播的,且周期T满足0.3s < T < 0.5s,则波的速度为_________m/s。