如图所示,一矩形线框竖直向上进入有水平边界的匀强磁场,磁场方向垂直纸
面向里,线框在磁场中运动时只受重力和磁场力,线框平面始终与
磁场方向垂直。向上经过图中1、2、3位置时的速率按时间依次为v1、v2、v3,向下经过图中2、1位置时的速率按时间依次为v4、v5,下列说法中一定正确的是( )
| A.v1>v2 | B.v2=v3 | C.v2=v4 | D.v4<v5 |
如图()所示,水平放置的两根平行金属导轨,间距
=0.3
.导轨左端连接
=0.6
的电阻,区域
内存在垂直于导轨平面
=0.6
的匀强磁场,磁场区域宽
="0.2"
.细金属棒
和
用长为2
=0.4
的轻质绝缘杆连接,放置在导轨平面上,并与导轨垂直,每根金属棒在导轨间的电阻均为
="0.3"
,导轨电阻不计,使金属棒以恒定速度
="1.0"
沿导轨向右穿越磁场,计算从金属棒
进入磁场(
=0)到
离开磁场的时间内,不同时间段通过电阻
的电流强度,并在图(
)中画出.

如图10所示,虚线框abcd内为一矩形匀强磁场区域,ab=2bc,磁场方向垂直于纸面;实线框a’b’c’d’是一正方形导线框,a’b’边与ab边平行。若将导线框匀速地拉离磁场区域,以W1表示沿平行于ab的方向拉出过程中外力所做的功,W2表示以同样速率沿平行于bc的方向拉出过程中外力所做的功,则( )

| A.W1=W2 | B.W2=2W1 | C.W1=2W2 | D.W2=4W1 |
如图,光滑斜面的倾角 = 30°,在斜面上放置一矩形线框abcd,ab边的边长l1 =" l" m,bc边的边长l2=" 0.6" m,线框的质量m =" 1" kg,电阻R = 0.1Ω,线框通过细线与重物相连,重物质量M =" 2" kg,斜面上ef线(ef∥gh)的右方有垂直斜面向上的匀强磁场,磁感应强度B =" 0.5" T,如果线框从静止开始运动,进入磁场最初一段时间是匀速的,ef线和gh的距离s =" 11.4" m,(取g = 10.4m/s2),求:
= 30°,在斜面上放置一矩形线框abcd,ab边的边长l1 =" l" m,bc边的边长l2=" 0.6" m,线框的质量m =" 1" kg,电阻R = 0.1Ω,线框通过细线与重物相连,重物质量M =" 2" kg,斜面上ef线(ef∥gh)的右方有垂直斜面向上的匀强磁场,磁感应强度B =" 0.5" T,如果线框从静止开始运动,进入磁场最初一段时间是匀速的,ef线和gh的距离s =" 11.4" m,(取g = 10.4m/s2),求:
(1)线框进入磁场前重物M的加速度;
(2)线框进入磁场时匀速运动的速度v;
(3)ab边由静止开始到运动到gh线处所用的时间t;
(4)ab边运动到gh线处的速度大小和在线框由静止开始到运动到gh线的整个过程中产生的焦耳热。
如图所示,a、b灯分别标有“36 V,40 W”和“36 V,25 W”,闭合电键,调节R,使a、b都正常发光。这时断开电键后再次闭合,则下列说法中正确的是( )
A.重新闭合瞬间,由于电感线圈对电流增大的阻碍作用, a将慢慢亮起来,而b立即变亮 a将慢慢亮起来,而b立即变亮 |
| B.重新闭合稳定后,两灯都正常发光,a的额定功率大,所以较亮 |
| C.断开瞬间,由于电感线圈对电流减小的阻碍作用,通过a的电流将逐渐减小,a渐渐变暗到熄灭 |
| D.断开瞬间,b灯立刻熄灭 |
如图所示,电感线圈L的直流电阻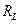 =1.0Ω,小灯泡的电阻
=1.0Ω,小灯泡的电阻 =5.0Ω,
=5.0Ω,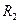 =4.0Ω,接在电动势E="24" V,内电阻可忽略的电路上.闭合开关S,待电路稳定后再断开开关,则在断开开关S的瞬间( )
=4.0Ω,接在电动势E="24" V,内电阻可忽略的电路上.闭合开关S,待电路稳定后再断开开关,则在断开开关S的瞬间( )
A. 支路上电流大小为4 A 支路上电流大小为4 A |
B.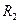 支路上电流大小为4A 支路上电流大小为4A |
C. 支路上电流大小为6A 支路上电流大小为6A |
D.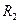 支路上电流大小为6A 支路上电流大小为6A |


| A.感应电流方向不变 |
| B.CD段直导线始终不受安培力 |
C.感应电动势最大值 |
D.感应电动势平均值 |
如图11-12所示,长为6m的导体AB在磁感强度B=0.IT的匀强磁场中,以AB上 的一点O为轴,沿着顺时针方向旋转。角速度ω=5rad/s,O点距A端为2m,求AB的电势差。
的一点O为轴,沿着顺时针方向旋转。角速度ω=5rad/s,O点距A端为2m,求AB的电势差。
一个共有10匝的闭合矩形线圈,总电阻为10Ω、面积为0.04m2,置于水平面上。若线框内的磁感强度在0.02s内,由垂直纸面向里,从1.6T均匀减少到零,再反向均匀增加到2.4T。则在此时间内,线圈内导线中的感应电流大小为______A,从上向下俯视,线圈中电流的方向为______时针方向。
长为a宽为b的矩形线圈,在磁感强度为B的匀强磁场中垂直于磁场的OO′轴以恒定的角速度ω旋转,设t= 0时,线圈平面与磁场方向平行,则此时的磁通量和磁通量的变化率分别是 [ ]
一矩形闭合线圈绕垂直于匀强磁场并位于线圈平面内的固定轴转动,下述说法正确的是( )
| A.穿过线圈的磁通量最大时,线圈中感应电流最大 |
| B.穿过线圈的磁通量为零时,线圈中感应电流最大 |
| C.若加大线圈的转速(其他条件不变),则线圈中交变电流的频率变大 |
| D.若加大线圈的转速(其他条件不变),则线圈中交变电流的最大值不变 |
如图所示,无限长金属导轨EF、PQ固定在倾角为θ=53°的光滑绝缘斜面上,轨道间距L="1" m,底部接入一阻值为R="0.4" Ω的定值电阻,上端开口.垂直斜面向上的匀强磁场的磁感应强度B="2" T.一质量为m="0.5" kg的金属棒ab与导轨接触良好,ab与导轨间动摩擦因数μ=0.2,ab连入导轨间的电阻r="0.1" Ω,电路中其余电阻不计.现用一质量为M="2.86" kg的物体通过一不可伸长的轻质细绳绕过光滑的定滑轮与ab相连.由静止释放M,不计空气阻力,当M下落高度h="2.0" m时,ab开始匀速运动(运动中ab始终垂直导轨,并接触良好).
(1)求ab棒沿斜面向上运动的最大速度.
(2)ab棒从开始运动到匀速运动的这段时间内电阻R上产生的焦耳热和流过电阻R的总电荷量是多少?
质量为m、带电荷量为+q的绝缘小球,穿在半径为r的光滑圆形轨道上,轨道平面水平.空间有分布均匀且随时间变化的磁场,磁场方向竖直向上,如图甲所示.磁感应强度B(t)的变化规律如图乙所示.
(1)若圆环由金属材料制成,求圆环上感应电动势E的大小;
(2)若圆环由绝缘材料制成,已知在t<T内,圆环处的感应电场的场强方向是沿顺时针并指向圆环的切线方向、大小为E′= ,t=0时刻小球静止.求t>T时,轨道对小球的作用力F的大小(小球重力不计).
,t=0时刻小球静止.求t>T时,轨道对小球的作用力F的大小(小球重力不计).
如右图所示,边长为L的正方形导线框质量为m,由距磁场H高处自由下落,其下边ab进入匀强磁场后,线圈开始做减速运动,直到其上边cd刚刚穿出磁场时,速度减为ab边进入磁场时的一半,磁场的宽度也为L.则线框穿越匀强磁场过程中产生的焦耳热为( )
| A.2mgL | B.2mgL+mgH |
C.2mgL+ mgH mgH |
D.2mgL+ mgH mgH |