如图所示,一根长度L的直导体棒中通过以大小为I的电流,静止放在导轨上,垂直于导体棒的匀强磁场的磁感应强度为B,B的方向与竖直方向成θ角,下列说法正确的是( )
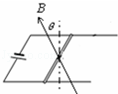
| A.导体棒受到磁场力大小为BLIsinθ |
| B.导体棒对轨道压力大小为mg﹣BILsinθ |
| C.导体棒受到导轨摩擦力为μ(mg﹣BILsinθ) |
| D.一个带电粒子沿垂直于磁场方向射入匀强磁场中,由于使沿途空气电离而使粒子的动能逐渐减小 |
如图所示,圆形区域内有垂直于纸面向里的匀强磁场,一个带电粒子以速度v从A点沿直径AOB方向射入磁场,经过△t时间从C点射出磁场,OC与OB成60°角,现将带点粒子的速度变为 ,仍从A点沿原方向射入磁场,不计重力,则粒子在磁场中的运动时间变为( )
,仍从A点沿原方向射入磁场,不计重力,则粒子在磁场中的运动时间变为( )

| A.3△t | B.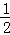 △t △t |
C.2△t | D. △t △t |
如图a、b、c为三个完全相同的带正电荷的油滴,在真空中从相同高度由静止下落到同一水平面,a下落中有水平匀强电场,b下落中有水平向里的匀强磁场,三油滴落地时间设为ta、tb、tc,落地时速度分别va、vb、vc,则( )
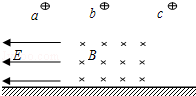
| A.ta=tb=tc,va=vb=vc | B.ta=tb=tc,va>vb=vc |
| C.tb>ta=tc,va=vb=vc | D.tb>ta=tc,va>vc=vb |
如图所示,有一垂直于纸面向外的有界匀强磁场,磁场的磁感应强度为B,其边界一边长L的正三角形(边界上有磁场)ABC为三角形的三个顶点,今有一质量为m、电荷量为+q的粒子(不计重力),以速度 ,从AB边上的某点P既垂直于AB边又垂直于磁场的方向射入,然后从BC边上某点Q射出,若从P点射入的粒子能从Q点射出,则
,从AB边上的某点P既垂直于AB边又垂直于磁场的方向射入,然后从BC边上某点Q射出,若从P点射入的粒子能从Q点射出,则
A. |
B. |
C. |
D. |
如图所示,在0≤x≤b、0≤y≤a的长方形区域中有一磁感应强度大小为B的匀强磁场,磁场的方向垂直于xOy平面向外。O处有一个粒子源,在某时刻发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xOy平面内的第一象限内。己知粒子在磁场中做圆周运动的周期为T,最先从磁场上边界中飞出的粒子经历的时间为 ,最后从磁场中飞出的粒子经历的时间为
,最后从磁场中飞出的粒子经历的时间为 。不计粒子的重力及粒子间的相互作用,则:( )
。不计粒子的重力及粒子间的相互作用,则:( )

A.粒子的射入磁场的速度大小 |
B.粒子圆周运动的半径 |
C.长方形区域的边长满足关系 |
D.长方形区域的边长满足关系 |
如图所示,长方体玻璃水槽中盛有NaCl的水溶液,在水槽左、右侧壁内侧各装一导体片,使溶液中通入沿x轴正向的电流I,沿y轴正向加恒定的匀强磁场B。图中a、b是垂直于z轴方向上水槽的前后两内侧面,则( )

A.a处电势高于b处电势
B.a处离子浓度大于b处离子浓度
C.溶液的上表面电势高于下表面的电势
D.溶液的上表面处的离子浓度大于下表面处的离子浓度
1957年,科学家首先提出了两类超导体的概念,一类称为I型超导体,主要是金属超导体,另一类称为Ⅱ型超导体(载流子为电子),主要是合金和陶瓷超导体。I型超导体对磁场有屏蔽作用,即磁场无法进入超导体内部,而Ⅱ型超导体则不同,它允许磁场通过。现将一块长方体Ⅱ型超导体通入稳恒电流I后放入匀强磁场中,如图所示。下列说法正确的是( )

| A.超导体的内部产生了热能 |
| B.超导体所受安培力等于其内部所有电荷定向移动所受洛伦兹力的合力 |
C.超导体表面上a、b两点的电势关系为 |
| D.超导体中电流I越大,a、b两点的电势差越大 |
一微粒质量为m带负电荷,电荷量大小是q,如图所示,将它以一定初速度在磁场中P点释放以后,它就做匀速直线运动,已知匀强磁场的磁感应强度为B,空气对微粒的阻力大小恒为f,则关于微粒做匀速直运动下列描述中正确的是 ( )

| A.微粒不可能沿竖直方向运动 |
| B.微粒可能沿水平方向运动 |
C.微粒做匀速运动时的速度v大小为 |
D.微粒做匀速运动时的速度v大小为 |
质谱仪是一种测定带电粒子质量或分析同位素的重要设备,它的构造原理如图示.离子源S产生的各种不同正离子束(速度可视为零),经MN间的加速电压U加速后从小孔S1垂直于磁感线进入匀强磁场,运转半周后到达照相底片上的P点.设P到S1的距离为x,则
| A.若离子束是同位素,则x越大对应的离子质量越小 |
| B.若离子束是同位素,则x越大对应的离子质量越大 |
| C.只要x相同,对应的离子质量一定相同 |
| D.只要x相同,对应的离子的电量一定相等 |
如图是某离子速度选择器的原理示意图,在一半径为R=10cm的圆形筒内有B=1×10-4T的匀强磁场,方向平行于圆的轴线.在圆柱形筒上某一直径两端开有小孔a、b分别作为入射孔和出射孔.现有一束比荷为q/m=2×1011C/kg的正离子,以不同角度α入射,最后有不同速度的离子束射出,其中入射角α=30°,且不经碰撞而直接从出身孔射出的离子的速度v大小是
| A.4×105m/s | B.4×106m/s | C.2×105m/s | D.2×106m/s |
两个电子以大小不同的初速度沿垂直于磁场的方向射入同一匀强磁场中,设R1、R2为这两个电子的运动轨道半径,T1、T2是它们的运动周期,则
| A.R1=R2,T1≠T2 | B.R1≠R2,T1≠T2 |
| C.R1=R2,T1=T2 | D.R1≠R2,T1=T2 |
三个速度大小不同的的同种带电粒子,沿如图所示长方形 区域匀强磁场的上边缘射入,当它们从下边缘飞出时,对入射方向的偏角分别为900、600、300,则它们在磁场中运动时间之比为

| A.1:1:1 | B.1:2:3 | C.3:2:1 | D. |
如图所示,两个半径相同的半圆形光滑轨道置于竖直平面内,左右两端点等高,分别处于沿水平方向的匀强电场和匀强磁场中。两个相同的带正电小球同时从两轨道左端最高点由静止释放。M、N为轨道的最低点。则下列分析正确的是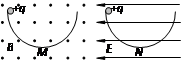
| A.两个小球到达轨道最低点的速度vM < vN |
| B.两个小球第一次经过轨道最低点时对轨道的压力FM > FN |
| C.小球第一次到达M点的时间小于小球第一次到达N点的时间 |
| D.磁场中小球能到达轨道另一端最高处,电场中小球不能到达轨道另一端最高处 |