如图所示,两根长直导线竖直平行固定放置,且与水平固定放置的光滑绝缘杆MN分别交于c、d两点,点o是cd的中点,杆MN上a、b两点关于o点对称。两导线均通有大小相等、方向向上的电流,已知长直导线在周围某点产生磁场的磁感应强度与电流成正比、与该点到导线的距离成反比。一带正电的小球穿在杆上,以初速度v0从a点出发沿杆运动到b点。在a、b、o三点杆对小球的支持力大小分别为Fa、Fb、Fo。下列说法可能正确的是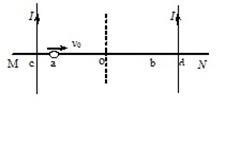
A.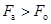 |
B.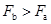 |
| C.小球一直做匀速直线运动 |
| D.小球先做加速运动后做减速运动 |
下列关于磁感应强度方向的说法中正确的是( )
| A.磁场中某处磁感应强度的方向就是该处磁场的方向 |
| B.某处磁感应强度的方向是一小段通电导线放在该处时所受磁场的安培力方向 |
| C.小磁针S极受的磁场力方向就是该处磁感应强度的方向 |
| D.垂直于磁场放置的通电导线的受力方向就是该处磁感应强度的方向 |
下列说法中正确的是( )
| A.点电荷就是体积和带电荷量都很小的带电体 |
B.根据F= ,当r→0时,可得出F→∞ ,当r→0时,可得出F→∞ |
C.由 可知,某处的磁感应强度的大小与放入该处的通电导线所受磁场力F成正比,与导线的I、L成反比 可知,某处的磁感应强度的大小与放入该处的通电导线所受磁场力F成正比,与导线的I、L成反比 |
| D.一小段通电导体在磁场中某处不受磁场力作用,该处磁感应强度不一定为零 |
光滑金属导轨宽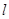 ="0.5" m,电阻不计,均匀变化的磁场充满整个轨道平面,如图甲所示。磁场的磁感应强度随时间变化的情况如图乙所示。金属棒ab的电阻为2
="0.5" m,电阻不计,均匀变化的磁场充满整个轨道平面,如图甲所示。磁场的磁感应强度随时间变化的情况如图乙所示。金属棒ab的电阻为2 ,垂直固定在导轨上静止不动,且与导轨左端距离
,垂直固定在导轨上静止不动,且与导轨左端距离 ="0.2" m。则( )
="0.2" m。则( )
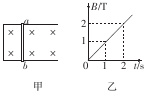
| A.1 s末回路中的电动势为0.l V |
| B.1 s末回路中的电流为1A |
| C.2 s内回路产生的电热为0. 01 J |
| D.2 s末,ab所受安培力大小为0.05 N |
无限长通电直导线在周围某一点产生的磁场的磁感应强度B的大小与电流成正比,与导线到这一点的距离成反比,即B=(式中k为常数)。如图所示,两根相距L的无限长直导线分别通有电流I和3I。在两根导线的连线上有a、b两点,a点为两根直导线连线的中点,b点距电流为I的导线的距离为L。下列说法正确的是 
| A.a点和b点的磁感应强度方向相同 |
| B.a点和b点的磁感应强度方向相反 |
| C.a点和b点的磁感应强度大小比为8∶1 |
| D.a点和b点的磁感应强度大小比为16∶1 |
光滑绝缘的水平桌面上方存在垂直桌面向上范围足够大的匀强磁场,虚线框abcd内(包括边界)存在平行于桌面的匀强电场,如图所示,一带电小球从d处静止开始运动,运动到b处时速度方向与电场边界ab平行,通过磁场作用又回到d点,已知bc=2ab=2L,磁感应强度为B,小球的质量为m,电荷量为q.则正确的是( )

| A.小球带正电 |
| B.小球从d到b做匀变速曲线运动 |
C.小球在虚线框外运动的速度大小为v= |
D.小球在b点时的加速度大小为a= |
下列可用来表示磁感应强度的单位关系的是( )
| A.1T=1kg/m2 | B.1T=1kg/( ) ) |
C.1T=1kg /( /( ) ) |
D.1T=1N/( ) ) |
已知通电长直导线周围某点的磁感应强度 ,即磁感应强度B与导线中的电流I成正比,与该点到导线的距离r成反比。如图所示两根平行长直导线相距为R,通以大小、方向均相同的电流,规定磁场方向垂直纸面向外为正,则在O﹣R区间内磁感应强度B随r变化的图线可能是( )
,即磁感应强度B与导线中的电流I成正比,与该点到导线的距离r成反比。如图所示两根平行长直导线相距为R,通以大小、方向均相同的电流,规定磁场方向垂直纸面向外为正,则在O﹣R区间内磁感应强度B随r变化的图线可能是( )


在通电螺线管内部有一点A,通过A点的磁感线方向一定是( )
| A.从螺线管的N极指向S极 |
| B.放在该点的小磁针北极受力的方向 |
| C.从螺线管的S极指向N极 |
| D.放在该点的小磁针的南极受力的方向 |
磁感应强度单位是特斯拉,1特斯拉相当于( )
| A.1kg/A·s2 | B.1kg·m/A·s2 |
| C.1kg·m2/s2 | D.1kg·m2/A·s2 |
下列说法不正确的是 ( )
| A.法拉第最先引入“场”的概念,并最早发现了电流的磁效应现象 |
| B.互感现象是变压器工作的基础 |
| C.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看做匀速直线运动,然后把各小段的位移相加,这应用了“微元法” |
D.电场强度 和 和 磁感应强度定义物理量的方法是比值定义法 磁感应强度定义物理量的方法是比值定义法 |
如图所示,一个边长L、三边电阻相同的正三角形金属框放置在磁感应强度为B的匀强磁场中.若通以图示方向的电流(从A点流入,从C点流出),电流强度I,则金属框受到的磁场力为( )

| A.0 | B.ILB | C. ILB ILB |
D.2ILB |
关于电荷量、电场强度、磁感应强度、磁通量的单位,下列说法错误的是( )
| A.牛/库是电场强度的单位 | B.特斯拉是磁感应强度的单位 |
| C.磁通量的单位是韦伯 | D.法拉是电荷量的单位 |