使两个完全相同的金属小球(均可视为点电荷)分别带上﹣3Q和+5Q的电荷后,将它们固定在相距为a的两点,它们之间库仑力的大小为F1.现用绝缘工具使两小球相互接触后,再将它们固定在相距为2a的两点,它们之间库仑力的大小为F2.则F1与F2之比为( )
| A.2:1 | B.4:1 | C.16:1 | D.60:1 |
真空中有两个点电荷,它们间的静电力为F,如果它们所带的电量都增大为原来的2倍,保持它们之间的距离不变,它们之间作用力的大小等于( )
| A.4F | B. |
C. |
D.2F |
在水平板上有M、N两点,相距D=0.45m,用长L=0.45m的轻质绝缘细线分别悬挂有质量m=´10-2kg、电荷量q=3.0´10-6C的小球(小球可视为点电荷,静电力常量 ),当两小球处于如图所示的平衡状态时
),当两小球处于如图所示的平衡状态时
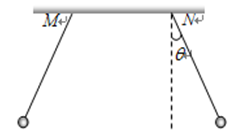
| A.细线与竖直方向的夹角q=30° |
| B.两小球间的距离为0.9m |
| C.细线上的拉力为0.2N |
| D.若两小球带等量异种电荷则细线与竖直方向的夹角q=30° |
两个用相同材料制成的半径相等的带电金属小球(可看成点电荷),其中一个球的带电量的绝对值是另一个的5倍,当它们静止于空间某两点时,静电力大小为F.现将两球接触后再放回原处,则它们间静电力的大小可能为( )
A.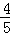 F F |
B.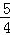 F F |
C. F F |
D.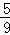 F F |
真空中有两个点电荷,它们间静电力为F,如果将它们所带的电量都增加到原来2倍,将它们之间的距离不变,它们之间的作用力大小等于
| A.F | B.3F | C.4F | D.6F |
真空中两个点电荷,电荷量分别为q1=8×10﹣9C和q2=﹣18×10﹣9C,两者固定于相距20cm的a、b两点上,如图所示.有一个点电荷放在a、b连线(或延长线)上某点,恰好能静止,则这点的位置是( )

| A.a点左侧40cm处 | B.a点右侧8cm处 |
| C.b点右侧20cm处 | D.以上都不对 |
两个点电荷相距为d,相互作用力大小 为F;保持两点电荷电荷量不变,改变它们之间的距离,使之相互作用力大小变为4F,则两点电荷之间的距离应变为( )
| A.4d | B.2d | C.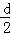 |
D.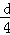 |
两个相同的金属小球,带电量之比为1:7,相距为r,两者相互接触后再放回原来的位置上,则他们间的库仑力可能为原来的( )
A.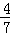 |
B. |
C.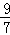 |
D. |
在光滑的绝缘水平面上,有一个正三角形abc,顶点a、b、c处分别固定一个正点电荷,电荷量相等,如图所示,D点为正三角形外接圆的圆心,E、G、H点分别为ab、ac、bc的中点,F点为E关于c电荷的对称点,则下列说法中正确的是( )

| A.D点的电场强度为零、电势可能为零 |
| B.E、F两点的电场强度等大反向、电势相等 |
| C.E、G、H三点的电场强度和电势均相同 |
| D.若释放c电荷,c电荷将一直做加速运动(不计空气阻力) |
真空中有相隔距离为r的两个点电荷,它们分别带4q和3q的电量,其间的静电力为F,如果保持它们之间的距离r不变,而将它们所带电量分别改变为8q和q,那么它们之间的静电力的大小应为( )
| A.2F | B. F F |
C.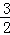 F F |
D. |
18世纪的物理学家发现,真空中两个点电荷间存在相互的作用.点电荷间的相互作用力跟两个点电荷的电荷量有关,跟它们之间的距离有关,发现这个规律的科学家是( )
| A.牛顿 | B.伽利略 | C.库仑 | D.法拉第 |
如图所示在光滑、绝缘的水平面上,沿一直线依次排列三个带电小球A、B、C(可视为质点).若它们恰能处于平衡状态.那么这三个小球所带的电荷量及电性的关系,下面的情况可能的是 ( )
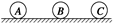
A.-9、4、-36 B.4、9、36 C.-3、2、8 D.3、-2、6
如图所示,光滑绝缘水平面上有三个带电小球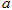 、
、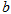 、
、 (均可视为点电荷),三球沿一条直线摆放,仅在它们之间的静电力作用下处于静止状态,则以下判断正确的是
(均可视为点电荷),三球沿一条直线摆放,仅在它们之间的静电力作用下处于静止状态,则以下判断正确的是
A.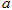 对 对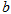 的静电力一定是引力 的静电力一定是引力 |
B.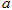 对 对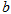 的静电力可能是斥力 的静电力可能是斥力 |
C.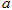 的电荷量可能比 的电荷量可能比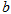 的少 的少 |
D.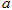 的电荷量一定比 的电荷量一定比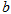 的多 的多 |