高中物理库仑定律试题

在真空中有两个带电小球，带电荷量分别是q₁和q₂，则()

A．电荷量大的小球受到的库仑力大	B．电荷量小的小球受到的库仑力大
C．两个小球受到的库仑力大小相等
D．只有q1=q2时，它们受到的库仑力的大小才相等

真空中两个同性的点电荷q₁、q₂ ,它们相距较近，保持静止。今释放q₂且q₂只在q₁的库仑力作用下运动，则q₂在运动过程中受到的库仑力：（）

A．不断减小	B．不断增加
C．始终保持不变	D．先增大后减小

日本物理学家小林诚和益川敏英由于发现了对称性破缺的起源，并由此预言的六个夸克逐渐被实验证实，获得2008年诺贝尔物理学奖．夸克之间的强相互作用势能可写为，式中r是正、反顶夸克之间的距离，a_s＝0．12是强相互作用耦合系数，k₂是与单位制有关的常数，在国际单位制中k₂=0．319×10^-25J·m；而在电荷之间的相互作用中，相距为r，电荷量分别为q₁q₂的两个点电荷之间的电势能，式中k₁是静电力常量．根据题中所给信息可以判定下列说法正确的是（）

A．正反顶夸克之间的相互作用力为

B．正反顶夸克之间的相互作用力为

C．若地球质量为M，则轨道半径为r，质量为m的地球卫星的万有引力势能为

D．若地球质量为M，则轨道半径为r、质量为m的地球卫星的万有引力势能为

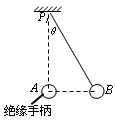
如图，悬挂在O点的一根不可伸长的绝缘细线下端有一个带电量不变的小球甲。在两次实验中，均缓慢移动另一带同种电荷的小球乙。当乙到达悬点O的正下方并与甲在同一水平线上，甲处于受力平衡时，悬线偏离竖直方向的角度为θ，若两次实验中乙的电量分别为q₁和q₂, θ分别为30°和45°。求：q₂ / q₁的值( 要求在右图中对甲进行受力分析)。

两个放在绝缘架上的相同金属球，相距为r ，球的半径比r小得多，带电量大小分别为q和3q，相互斥力为3F。现将这两个金属球相接触，然后分开，仍放回原处，则它们之间的相互作用力将变为_________F。

在光滑绝缘的水平面上，有两个相距较近的带同种电荷的小球，将它们由静止释放，则两球间

A．距离变大，库仑力变大	B．距离变小，库仑力变大
C．距离变大，库仑力变小	D．距离变小，库仑力变小

两个质量均为m=2×10-⁶kg的小球，悬于长l=60cm的细丝线上．丝线的另一点固定于同一点O．当使两球带上等量同种电荷后，两球互相排斥使两丝线间形成α=90°的夹角(图)．求每个小球的带电量．

两个相同的金属小球，带电量之比为1∶5，当它们相距r时的相互作用力为F₁．若把它们互相接触后再放回原处，它们的相互作用力变为F_2.则F₁/F₂为 ( )

A．5∶1．

B．5∶9．

C．5∶4．

D．5∶8．

真空中有两个静止的点电荷，它们之间静电力的大小为F。如果保持这两个点电荷之间的距离不变，而将它们的电荷量都变为原来的3倍，那么它们之间静电力的大小变为

在真空中有两个点电荷，它们之间的静电力为F。如果保持它们之间的距离不变，将它们各自所带的电荷量减小到原来的一半，那么它们之间静电力的大小等于

A．4F

B．2F

C．

D．

某研究性学习小组在探究电荷间的相互作用与哪些因素有关时，设计了以下实验：
（1）该组同学首先将一个带正电的球体A固定在水平绝缘支座上。把系在绝缘细线上的带正电的小球B（图中未画出）先后挂在图中P₁、P₂、P₃位置，比较小球在不同位置所受带电体的作用力的大小。同学们根据力学知识分析得出细线偏离竖直方向的角度越小，小球B所受带电球体A的作用力（填“越大”或“越小”或“不变”），实验发现小球B在位置细线偏离竖直方向的角度最大（填“P₁或P₂或P₃”）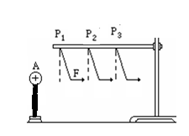

（2）接着该组同学使小球处于同一位置，增大或减少小球A所带的电荷量，比较小球所受作用力大小的变化。如图，悬挂在P₁点的不可伸长的绝缘细线下端有一个带电量不变的小球B。在两次实验中，均缓慢移动另一带同种电荷的小球A。当A球到达悬点P₁的正下方并与B在同一水平线上B处于受力平衡时，悬线偏离竖直方向角度为θ。若两次实验中A的电量分别为q₁和q₂，θ分别为30°和45°，则q₂/q₁为（）
A．2 B．3 C． D．

一个带+3q和一个带-q的大小完全相同的金属球，相距为r时作用力为F，若把它们相接触后再放到相距为r的地方，假设两种情况下金属球上的电荷都是均匀分布的，这时它们之间的作用力的大小将变为：

A．F

B．F

C．F

D．3F

一个挂在绝缘丝线下端的带电的小球B，静止在图示位置。若固定的带正电的小球A电量为Q，B球的质量为m，带电量为q，θ=45°，A和B在同一水平线上，整个装置处于真空中，A、B球均可视为点电荷，求：

（1）B球带何种电？
（2）A、B两球之间的距离为多少?

如图所示，一长为L的绝缘细线下端系质量为m的金属小球，并带有 -q的电荷量，在细线的悬点o处放一带电荷量为+q的点电荷。要使金属球能在竖直平面内做完整的圆周运动，求：
（1）金属球在最高点的最小速度值是多大？
（2）如果金属球刚好通过最高点，则它通过最低点时的速度多大？

如图9所示，在无限长的光滑绝缘的水平直轨道上有两个带电小球a和b，a球品质为2m，带电量为＋q，b球品质为m，带电量＋2q，两球相距较远且相向运动，某时刻a、b球的速度大小依次为v和1.5v，由于静电斥力的作用，它们不会相碰，则下列叙述正确的是（）

A．两球相距最近时，速度大小相等、方向相同

B．a球与b球所受的静电斥力对两球始终做负功

C．a球一直沿原方向运动，b球要反向运动

D．a、b两球都要反向运动，但a球先反向