半圆形光滑轨道固定在水平地面上,使其轨道平面与地面垂直,物体m1、m2同时由轨道左、右最高点释放,二者碰后黏在一起向左运动,最高能上升到轨道上M点,如图所示.已知OM与竖直方向夹角为60°,则两物体的质量之比为m1∶m2为( )
A.( +1)∶( +1)∶( -2) -2) |
B. ∶1 ∶1 |
C.( -1)∶( -1)∶( +1) +1) |
D.1∶ |
在光滑水平地面上有两个相同的弹性小球A、B,质量都是m,现B球静止,A球向B球运动,发生正碰.已知碰撞过程总机械能守恒,两球压缩最紧时弹性势能为Ep,则碰前A球速度等于( )
A. B.
B. C.2
C.2 D.
D.
如下图所示,一轻弹簧左端固定在长木板M的左端,右端与小木块m连接,且m、M及M与地面间接触光滑.开始时,m和M均静止,现同时对m、M施加等大反向的水平恒力F1和F2,从两物体开始运动以后的整个运动过程中,弹簧形变不超过其弹性限度.对于m、M和弹簧组成的系统( )
| A.由于F1、F2等大反向,故系统机械能守恒 |
| B.当弹簧弹力大小与F1、F2大小相等时,m、M各自的动能最大 |
| C.由于F1、F2大小不变,所以m、M各自一直做匀加速运动 |
| D.由于F1、F2等大反向,故系统的动量始终为零 |
质量为m的小球A,沿光滑水平面以速度v0与质量为2m的静止小球B发生正碰撞,碰撞后A球的动能变为原来的 ,那么小球B的速度可能是( )
,那么小球B的速度可能是( )
A. v0 v0 |
B. v0 v0 |
C. v0 v0 |
D. v0 v0 |
小球D在光滑水平面上以相同的速率分别与原来静止的三个小球A、B、C相碰(A、B、C与D等大).D与A碰后,D被反弹回来.D与B碰后,D静止不动.D与C碰后,D继续沿原方向运动.D与A、B、C在碰撞过程中的动能损失均忽略不计,则( )
A.碰后A球获得的动量最大,获得的动能也最大
B.碰后B球获得的动量最大,获得的动能也最大
C.碰后C球获得的动量最大,B球获得的动能最大
D.碰后A球获得的动量最大,B球获得的动能最大
(1)如图1所示,为一固定在竖直平面内的光滑轨道,
段水平,
段与
段平滑连接。质量为
的小球从高位
处由静止开始沿轨道下滑,与静止在轨道
段上质量为
的小球发生碰撞,碰撞后两球两球的运动方向处于同一水平线上,且在碰撞过程中无机械能损失。求碰撞后小球
的速度大小
。

(2)碰撞过程中的能量传递规律在屋里学中有着广泛的应用。为了探究这一规律,我们才用多球依次碰撞、碰撞前后速度在同一直线上、且无机械能损失的恶简化力学模型。如图2所示,在固定光滑水平轨道上,质量分别为的若干个球沿直线静止相间排列,给第1个球初能
,从而引起各球的依次碰撞。定义其中第
个球经过依次碰撞后获得的动能
与
之比为第1个球对第
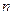 个球的动能传递系数
个球的动能传递系数。
a.求;
b.若为确定的已知量。求
为何值时,
值最大。
