下列几种现象中,动量不守恒的是
| A.在光滑水平面上两球发生碰撞 |
| B.车原来静止在光滑的水平面上,车上的人从车头走到车尾 |
| C.水平放置的弹簧一端固定,另一端与置于光滑水平面的物体相连,伸长的弹簧拉物体运动 |
| D.火箭的反冲运动 |
.下列几种现象中,动量不守恒的是
| A.在光滑水平面上两球发生碰撞 |
| B.车原来静止在光滑的水平面上,车上的人从车头走到车尾 |
| C.水平放置的弹簧一端固定,另一端与置于光滑水平面的物体相连,伸长的弹簧拉物体运动 |
| D.火箭的反冲运动 |
如图,竖直固定轨道abcd段光滑,长为L=1.0m的平台de段粗糙,abc段是以O为圆心的圆弧.小球A和B紧靠一起静止于e处,B的质量是A的4倍.两小球在内力作用下突然分离,A分离后向左始终沿轨道运动, 与de段的动摩擦因数μ=0.2,到b点时轨道对A的支持力等于A的重力的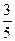 , B分离后平抛落到f点,f到平台边缘的水平距离S= 0.4m,平台高h=0.8m,g取10m/s2,求:
, B分离后平抛落到f点,f到平台边缘的水平距离S= 0.4m,平台高h=0.8m,g取10m/s2,求:
(1)AB分离时B的速度大小vB;
(2)A到达d点时的速度大小vd;
(3)圆弧 abc的半径R.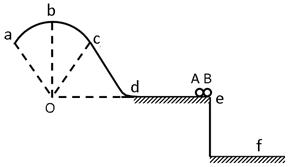
如图16,一质量为m 的物块静止在桌面边缘,桌面离水平地面的高度为h。一质量也为m 的子弹以水平速度v0射入物块后,以水平速度v0/2射出,重力加速度为g。求:
(1)子弹射出瞬间物块的速度;
(2)子弹射穿物块过程中 系统损失的机械能;
系统损失的机械能;
(3)物块落地点离桌面边缘的水平距离. 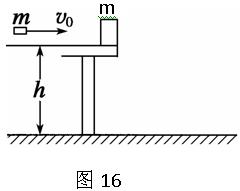
如图所示,水平地面上静止放置着物块B和C,相距l=1.0m。物块A以速度v0=10m/s沿水平方向与B正碰。碰撞后A和B牢固地粘在一起向右运动,并再与C发生正碰,碰后瞬间C的速度v=2.0m/s。已知A和B的质量均为 ,C的质量为A质量的K倍,物块与地面的动摩擦因数μ=0.45。(设碰撞时间很短,
,C的质量为A质量的K倍,物块与地面的动摩擦因数μ=0.45。(设碰撞时间很短, 取10m/s2)
取10m/s2)
(1)计算与C碰撞前瞬间AB的速度;
(2)根据AB与C的碰撞过程分析K的取值范围,并讨论与C碰撞后AB的可能运动方向。
质量为M,长为L的小车静止在光滑的水平面上,质量为m的小物块放在小车的最左端,现有一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动。物块和小车之间的摩擦力为f。经过时间t,小车的位移为s,物块刚好滑到小车的最右端。则以下说法正确的是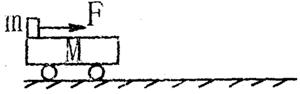
| A.此时物块的动能为(F-f)(s+L) |
| B.此时物块的动量为Ft |
| C.这一过程中物块和小车增加的动能为Fs |
| D.这一过程中物块和小车减少的机械能为fL |
如图12所示,A为一具有光滑曲面的固定轨道,轨道底端是水平的,质量M=40kg的上车B静止于轨道右侧,其板面与轨道底端靠近且在同一水平面上,一个质量m="20" kg,可视为质点的小滑块C以 的初速度从轨道顶端滑下,C冲上小车B后,经一段时间与小车相对静止并继续一起运动。若轨道顶端与底端水平面的高度差为
的初速度从轨道顶端滑下,C冲上小车B后,经一段时间与小车相对静止并继续一起运动。若轨道顶端与底端水平面的高度差为 ,C与小车板面间的动摩擦因数为
,C与小车板面间的动摩擦因数为 ,小车与水平面间的摩擦不计,
,小车与水平面间的摩擦不计, 取10m/s2。求
取10m/s2。求
(1)C与小车保持相对静止时的速度大小。
(2)从C冲上小车瞬间到与小车相对静止瞬间所用的时间。
(3)C冲上小车后相对于小车板面滑动的距离。
如图所示,在光滑水平的地面上,有一辆上表面光滑的正在以速度 向右运动的小车,车上的木块一样与车一起以
向右运动的小车,车上的木块一样与车一起以 向右运动,车左端有一固定挡板P,挡板和车的质量为M=16kg,在挡板P和质量为M=9kg的木块之间有少量炸药,炸药爆炸提供给小车和木块的总机械能为E0=1800J.若要使炸药爆炸后木块的动能等于E0,在爆炸前小车的速度
向右运动,车左端有一固定挡板P,挡板和车的质量为M=16kg,在挡板P和质量为M=9kg的木块之间有少量炸药,炸药爆炸提供给小车和木块的总机械能为E0=1800J.若要使炸药爆炸后木块的动能等于E0,在爆炸前小车的速度 为多少?
为多少? 
如图,在光滑水平面上并排放置的木块A、B,已知 ,
, 。A木块长为
。A木块长为 。现有质量
。现有质量 的小物块C以初速度
的小物块C以初速度 在A表面沿水平方向向右滑动,由于C与A、B均有摩擦,且动摩擦因素为
在A表面沿水平方向向右滑动,由于C与A、B均有摩擦,且动摩擦因素为 。C最终停在B上,B、C最后的共同速度
。C最终停在B上,B、C最后的共同速度 。求:
。求:
(1)A木块的最终速度的大小。
(2)C木块滑离A木块时的速度大小。
(3)试求B木块的长度至少多长。
在用如图所示的装置验证动量守恒的试验中
(1)在验证动量守恒定律的实验中,必须要求的条件是:( )
A、轨道是光滑的。
B、轨道末端的切线是水平的。
C、m1和m2的球心在碰撞的瞬间在同一高度。
D、碰撞的瞬间m1和m2球心连线与轨道末端的切线平行。
E、每次m1都要从同一高度静止滚下。
(2)在验证动量守恒定律的实验中,必须测量的量有:( )
A、小球的质量m1和m2。 B、小球的半径r。
C、桌面到地面的高度H。 D、小球m1的起始高度h。
E、小球从抛出到落地的时间t。 F、小球m1未碰撞飞出的水平距离。
G、小球m1和m2碰撞后飞出的水平距离。
(3)实验时,小球的落点分别如右图的M、N、P点,应该比较下列哪两组数值在误差范围内相等,从而验证动量守恒定律:( )
A、m1· 。 B、m1·
。 B、m1· 。
。
C、m1· 。 D、m1·
。 D、m1· +m2·
+m2· 。
。
E、m1· +m2·(
+m2·(
 )。 F、m1·
)。 F、m1· +m2·(
+m2·(
 )。
)。
如图所示,一个下面装有轮子的贮气瓶停放在光滑的水平地面上,左端与竖直墙壁接触.现打开右端阀门K,气体往外喷出,设喷口面积为S,气体密度为r,气体往外喷出的速度为v,则气体刚喷出时钢瓶左端对竖直墙的作用力大小是
| A.rnS | B. |
C. |
D.rn2S |
(12分)木板与水平面间的动摩擦因数μ为0.24,木板右端放着质量mB为1.0 kg的小物块B(视为质点),它们均处于静止状态.木板突然受到水平向右的12 N·s的瞬时冲量I作用开始运动,当小物块滑离木板时,木板的动能EKA为8.0 J,小物块的动能EKB为0.50 J,重力加速度取10 m/s2,求:
(1)瞬时冲量作用结束时木板的速度v0;
(2)木板的长度L.
一炮弹质量为m,相对水平方向以一定的倾角θ斜向上发射,发射速度为v,炮弹在最高点爆炸成两块,其中一块沿原轨道返回,质量为 ,求:
,求:
(1)另一块爆炸后瞬时的速度大小;
(2)爆炸过程系统增加的机械能。
如图所示是用频闪照相的方法拍摄到的一个弹簧振子的振动情况,甲图是振子静止在平衡位置时的照片,乙图是振子被拉到左侧距平衡位置20 cm处放手后向右运动 周期内的频闪照片,已知频闪的频率为10 Hz,则下列说法正确的是
周期内的频闪照片,已知频闪的频率为10 Hz,则下列说法正确的是
| A.该振子振动的周期为1.6 s |
| B.该振子振动的周期为1.2 s |
| C.振子在该 1/4周期内做加速度逐渐减小的变加速运动 |
| D.从图乙可以看出再经过0.2 s振子将运动到平衡位置右侧10 cm处 |