如图4质量为m的物体A放置在质量为M的物体B上,B与弹簧相连,它们一起在光滑水平面上作简谐振动,振动过程中A、B之间无相对运动.设弹簧的倔强系数为k.当物体离开平衡位置的位移为x时,A、B间摩擦力的大小等于( )
A.0; B.kx; C.kx m/M D.kx m/(M+m)
关于简谐运动,以下说法正确的是( )
| A.只要回复力的方向总是指向平衡位置,物体就做简谐运动 |
| B.加速度的方向总是与位移的方向相反 |
| C.质点的位移与时间的关系遵从正弦函数规律 |
| D.速度方向有时与位移方向相反,有时与位移方向相同 |
沿水平方向振动的弹簧振子,如图所示,可能的受力情况是( )
A.重力,支持力和弹簧的弹力
B重力,支持力,弹簧的弹力和回复力
C. 重力,支持力和回复力
D. 重力,支持力,摩擦力和回复力
一根弹簧原长为L0,挂一质量为m的物体时伸长量为x,把它们共同套在一根光滑水平杆上组成弹簧振子,当其振幅为A时,物体振动的最大加速度是______________。
如图所示,弹簧振子在振动过程中,经过a、b两点的速度相同,历时0.2s。从b点再回到a的最短时间为0.4s,则该振子的振动频率为( )
| A.1Hz | B.1.25Hz |
| C.2Hz | D.2.5Hz |

弹簧振子在光滑水平面内做简谐运动,在振子向平衡位置运动的过程中,下列说法正确的是( )
| A.振子所受的回复力逐渐增大 |
| B.振子的位移逐渐增大 |
| C.振子的速度逐渐减小 |
| D.振子的加速度逐渐减小 |
如图一轻弹簧与一物体组成弹簧振子,物体在同一条竖直线上的A、B间作简谐振动,O点为平衡位置,C为AO的中点,已知OC=h,振子周期为T,某时刻物体恰好经过C点并向上运动,则从此时刻开始计时 ( )
A.t=T/4时刻,物体回到C点
B.△t=T/2时间内,物体运动的路程为4h
C.t=3T/8时刻,物体的振动位移为0
D.t=3T/8时刻,物体的振动速度方向向下
如图所示,小球P连接着轻质弹簧,放在光滑水平面上,弹簧的另一端固定在墙上,O点为它的平衡位置,把P拉到A点,使OA=1cm,静止释放,经0.4s小球第1次到达O点。如果把P拉到A′点,使OA′=2cm,则由静止释放后小球第一次运动到O点所需的时间
| A.0.2s | B.0.4s |
| C.0.6s | D.0.8s |
弹簧振子以O点为平衡位置,在B、C两点间做简谐运动.在t=0时刻,振子从O、B间的P 点以速度v向B点运动;在t="0.20" s时,振子速度第一次变为-v;在t="0.50" s时,振子速度第二次变为-v.
(1)求弹簧振子振动的周期T;
(2)若B、C之间的距离为25 cm,求振子在4.0 s内通过的路程.
如图所示,轻质弹簧下挂重为300N的物体A,弹簧伸长了3cm,再挂上重为200N的物体B时又伸长了2cm,弹簧均在弹性限度内。若将连接A、B两物体的细绳烧断,使 A在竖直面内做简谐运动,下列说法中正确的是
A.振幅为5cm
B.振幅为2cm
C.最大回复力为200N
D.当物体A振动到最高点时,弹簧处于压缩状态
弹簧振子在做简谐运动,则下列说法中正确的是
| A.振子每次通过同一位置时其速度相同 |
| B.振子每次通过同一位置时其位移相同 |
| C.振子每次通过同一位置时其加速度可能不同 |
| D.振子通过平衡位置时所受合外力一定为零 |
如图所示,小球从高处下落一段距离后到竖直放置下端固定的轻弹簧上,从小球接触弹簧开始至弹簧压缩到最短的整个过程中,下列关于机械能的叙述中正确的是:
| A.重力势能和动能之和一直减小 |
| B.重力势能和弹性势能之和一直增大 |
| C.动能和弹性势能之和保持不变 |
| D.重力势能、弹性势能和动能之和总保持不变 |
如图所示,某均匀介质中各质点的平衡位置在同一条直线上,相邻两点间的距离为1m。t = 0时,波源S开始振动,速度方向竖直向上,振动由此以1m/s的速度开始向右传播。t = 1.0s时,波源S第一次到达波峰处。由此可以判断,t =7.0s时( )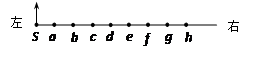
| A.质点b达到最大速度 |
| B.质点c达到最大加速度 |
| C.质点e速度方向竖直向下 |
| D.质点h正好到达波谷位置 |
下列关于简谐振动和简谐波的说法,正确的是( )
| A.媒质中质点振动的周期一定和相应的波的周期相等 |
| B.媒质中质点振动的速度一定和相应的波的波速相等 |
| C.波的传播方向一定和媒质中质点振动的方向一致 |
| D.横波的波峰与波谷在振动方向上的距离一定是质点振幅的两倍 |