一物体从某一高度自由下落,落在直立于地面的轻弹簧上,如图所示.在A点,物体开始与弹簧接触,到B点时,物体速度为零,然后被弹回.下列说法中正确的是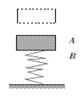
| A.物体从A下降到B的过程中,速率先增大后减小 |
| B.物体从B上升到A的过程中,速率不断变大 |
| C.物体在B点时,所受合力为零 |
| D.物体从A下降到B的过程中,加速度先减小后增大 |
如图所示,直杆长L1=0.5m,圆筒高为L2=3.7m。直杆位于 圆筒正上方H=0.8m处。直杆从静止开始做自由落体运动,并能竖直穿越圆筒。试求(取g=10m/s2)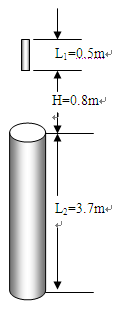
(1)由释放到直杆下端刚好开始进入圆筒时经历的时间t1
(2)直杆穿越圆筒所用的时间t.
如图所示,一根长为l的轻质软绳一端固定在O点,另一端与质量为m的小球连接,初始时将小球放在与O点等高的A点,OA= ,现将小球由静止状态释放,则当小球运动到O点正下方时,绳对小球拉力为( )(已知:sin37°=0.6,cos37°=0.8)
,现将小球由静止状态释放,则当小球运动到O点正下方时,绳对小球拉力为( )(已知:sin37°=0.6,cos37°=0.8)
| A.2mg | B.3mg | C. |
D. |
一宠物毛毛狗“乐乐”在玩耍时不慎从离地h1=19.5m高层阳台无初速度竖直掉下,当时刚好是无风天气,设它的质量m=2kg,在“乐乐”开始掉下的同时,几乎在同一时刻刚好被地面上的一位保安发现并奔跑到达楼下,奔跑过程用时2.5s,恰好在距地面高度为h2=1.5m处接住“乐乐”, “乐乐”缓冲到地面时速度恰好为零,设“乐乐”下落过程中空气阻力为其重力的0.6倍,缓冲过程中空气阻力为其重力的0.2倍,重力加速度g=10m/s2。求:
(1)为了营救“乐乐”允许保安最长的反应时间;
(2)在缓冲过程中保安对“乐乐”做的功。
如图 所示,小物体从竖直弹簧上方离地高
所示,小物体从竖直弹簧上方离地高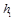 处由静止释放,其动能
处由静止释放,其动能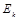 与离地高度
与离地高度 的关系如图
的关系如图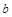 所示.其中高度从
所示.其中高度从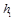 下降到
下降到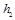 ,图象为直线,其余部分为曲线,
,图象为直线,其余部分为曲线,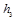 对应图象的最高点,轻弹簧劲度系数为
对应图象的最高点,轻弹簧劲度系数为 ,小物体质量为
,小物体质量为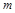 ,重力加速度为
,重力加速度为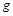 .以下说法正确的是( )
.以下说法正确的是( )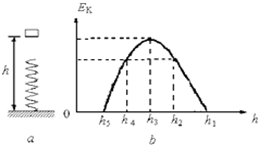
A.小物体下降至高度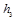 时,弹簧形变量为0 时,弹簧形变量为0 |
B.小物体下落至高度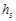 时,加速度为0 时,加速度为0 |
C.小物体从高度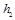 下降到 下降到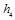 ,弹簧的弹性势能增加了 ,弹簧的弹性势能增加了 |
D.小物体从高度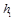 下降到 下降到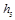 ,弹簧的最大弹性势能为 ,弹簧的最大弹性势能为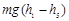 |
甲、乙两球质量分别为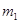 、
、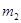 ,从同一地点(足够高)处同时由静止释放。两球下落过程所受空气阻力大小
,从同一地点(足够高)处同时由静止释放。两球下落过程所受空气阻力大小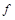 仅与球的速率
仅与球的速率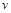 成正比,与球的质量无关,即
成正比,与球的质量无关,即 (
(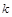 为正的常量)。两球的
为正的常量)。两球的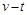 图象如图所示。落地前,经时间
图象如图所示。落地前,经时间 两球的速度都已达到各自的稳定值
两球的速度都已达到各自的稳定值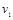 、
、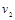 。则下列判断正确的是 ( )
。则下列判断正确的是 ( )
| A.释放瞬间甲球加速度较大 |
B.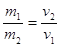 |
| C.甲球质量大于乙球 |
D.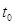 时间内两球下落的高度相等 时间内两球下落的高度相等 |
气球以10 m/s的速度匀速竖直上升,从气球里掉下一个物体,经17 s物体到达地面,则物体脱离气球时的高度为(取g=10 m/s2)
| A.1275m | B.800m | C.1445 m | D.500 m |
在离地高h处,沿竖直方向同时向上和向下抛出两个小球,它们的初速度大小均为v,不计空气阻力,两球落地的时间差为
A.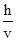 |
B. |
C. |
D.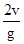 |
如图a所示,小物体从竖直弹簧上方离地高h1处由静止释放,其动能Ek与离地高度h的关系如图b所示.其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,小物体质量为m,重力加速度为g。以下说法正确的是( )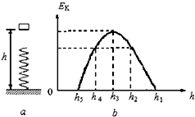
| A.小物体下降至高度h3时,弹簧形变量为0 |
| B.小物体下落至高度h5时,加速度为0 |
C.小物体从高度h2下降到h4,弹簧的弹性势能增加了 |
D.小物体从高度h1下降到h5,弹簧的最大弹性势能为 |
如图所示,竖直放置的质量为4m,,长为L的圆管顶端塞有一个质量为m的弹性圆球,球和管间的滑动摩擦力和最大静摩擦力大小均为4mg.圆管从下端离地面距离为H处自由落下,落地后向上弹起的速度与落地时速度大小相等。试求: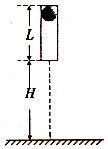
(1)圆管弹起后圆球不致滑落,L应满足什么条件;
(2)圆管上升的最大高度是多少;
(3)圆管第二次弹起后圆球不致滑落,L又应满足什么条件。
如图所示为“割绳子”游戏中的一幅截图,游戏中割断左侧绳子糖果就会通过正下方第一颗星星…….糖果一定能经过星星处吗?现将其中的物理问题抽象出来进行研究:三根不可伸长的轻绳共同系住一颗质量为m的糖果(可视为质点),设从左到右三根轻绳的长度分别为l1、l2和l3,其中最左侧的绳子处于竖直且张紧的状态,另两根绳均处于松弛状态,三根绳的上端分别固定在同一水平线上,且相邻两悬点间距离均为d,糖果正下方的第一颗星星与糖果距离为h。已知绳子由松弛到张紧时沿绳方向的速度分量即刻减为零,现将最左侧的绳子割断,以下选项正确的是
A.只要满足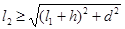 ,糖果就能经过正下方第一颗星星处 ,糖果就能经过正下方第一颗星星处 |
B.只要满足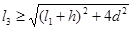 ,糖果就能经过正下方第一颗星星处 ,糖果就能经过正下方第一颗星星处 |
C.糖果可能以 的初动能开始绕中间悬点做圆运动 的初动能开始绕中间悬点做圆运动 |
D.糖果到达最低点的动能可能等于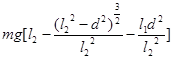 |
如图所示,长L=1.5 m、高h=0.45 m、质量M=10 kg的长方体木箱在水平面上向右做直线运动.当木箱的速度v0=3.6 m/s时,对木箱施加一个方向水平向左的恒力F=50 N,并同时将一个质量m=1 kg的小球轻放在木箱上距右端处的P点(小球可视为质点,放在P点时相对于地面间的速度为零),经过一段时间,小球脱离木箱落到地面.已知木箱与地面间的动摩擦因数μ=0.2,而小球与木箱之间的摩擦不计.取g=10 m/s2,求:
(1)小球从开始离开木箱至落到地面所用的时间;
(2)小球放上P点后,木箱向右运动的最大位移;
(3)小球离开木箱时,木箱的速度.
如图所示,一位质量为 m =" 65" kg的特技演员,在进行试镜排练时,从离地面高 h1="6" m高的楼房窗口跳出后竖直下落,若有一辆平板汽车正沿着下落点正下方所在的水平直线上,以v0=" 6" m/s的速度匀速前进.已知该演员刚跳出时,平板汽车恰好运动到其前端距离下落点正下方3 m处,该汽车车头长2 m,汽车平板长4.5 m,平板车板面离地面高 h2 ="1" m,人可看作质点,g取10 m/s2,人下落过程中未与汽车车头接触,人与车平板间的动摩擦因数μ=0.2。问: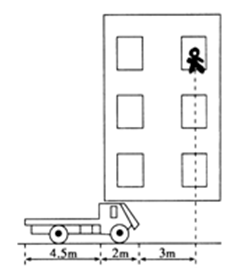
(1)人将落在平板车上距车尾端多远处?
(2)假定人落到平板上后立即俯卧在车上不弹起,司机同时使车开始以大小为 a车 ="4" m/s2的加速度做匀减速直线运动,直至停止,则人是否会从平板车上滑下?
(3)人在货车上相对滑动的过程中产生的总热量Q为多少?