高中物理万有引力定律及其应用试题

2010年10月1日，“嫦娥二号”卫星在西昌卫星发射中心成功发射，标志着我国航天事业又取得巨大成就．卫星发射过程中，假设地～月转移轨道阶段可以简化为：绕地球做匀速圆周运动的卫星，在适当的位置P点火，进入Q点后被月球俘获绕月球做匀速圆周运动，已知月球表面重力加速度为g，月球半径为R，“嫦娥二号”绕月球做匀速圆周运动的轨道半径为r，从发射“嫦娥二号”到在绕月轨道上正常运行，其示意图如图所示，则下列说法正确的是（ ）

A．在Q点启动火箭向运动方向喷气

B．在P点启动火箭向运动方向喷气

C．“嫦娥二号”在绕月轨道上运行的速率为

D．“嫦娥二号”在绕月轨道上运行的速率为

质量为m的卫星发射前静止在地球赤道表面。假设地球可视为质量均匀分布的球体，半径为R。
（1）已知地球质量为M，自转周期为T，引力常量为G。求此时卫星对地表的压力N的大小；
（2）卫星发射后先在近地轨道上运行（轨道离地面的高度可以忽略不计），运行的速度大小为v₁，之后经过变轨成为地球的同步卫星，此时离地面高度为H，运行的速度大小为v₂。
a．求比值；
b．若卫星发射前随地球一起自转的速度大小为v₀，通过分析比较v₀、 v₁、v₂三者的大小关系。

2013年12月2日1时30分，嫦娥三号探测器由长征三号乙运载火箭从西昌卫星发射中心发射，首次实现月球软着陆和月面巡视勘察。嫦娥三号的飞行轨道示意图如图所示。假设嫦娥三号在环月段圆轨道和椭圆轨道上运动时，只受到月球的万有引力，则（    )

A．若已知嫦娥三号环月段圆轨道的半径、运动周期和引力常量，则可算出月球的密度

B．嫦娥三号由环月段圆轨道变轨进入环月段椭圆轨道时，应让发动机点火使其减速

C．嫦娥三号在环月段椭圆轨道上P点的速度大于Q点的速度

D．嫦娥三号在动力下降阶段，其引力势能减小

某人造地球卫星在近似圆轨道上运行的过程中，由于轨道所在处的空间存在极其稀薄的空气，则

A．如不加干预，卫星所受的万有引力将越来越小

B．如不加干预，卫星运行一段时间后动能会增加

C．卫星在近似圆轨道上正常运行时，由于失重现象卫星内的物体不受地球引力作用

D．卫星在近似圆轨道上正常运行时，其速度介于第一宇宙速度和第二宇宙速度之间

研究发现，月球的平均密度和地球的平均密度差不多相等，航天飞机分别贴近月球表面和地球表面飞行，下列哪些物理量的大小差不多相等的是（ ）

A．线速度

B．角速度

C．向心加速度

D．万有引力

已知地球质量为M，半径为R，自转周期为t，地球同步卫星质量为m，引力常量为G。有关同步卫星，下列表述正确的是

A．卫星运行的向心加速度小于地球表面的重力加速度

B．卫星的运行速度小于第一宇宙速度

C．卫星运行时受到的向心力大小为

D．卫星距地面的高度为

已知引力常量G和以下各组数据，不能够计算出地球质量的是（     ）

A．地球绕太阳运行的周期和地球与太阳间的距离

B．月球绕地球运行的周期和月球与地球间的距离

C．人造地球卫星在地面附近处绕行的速度与周期

D．若不考虑地球的自转，已知地球的半径与地面的重力加速度

2013年10月13日航天员在绕地球圆周运动的神舟六号上进行了预定的科学试验．下面是一中学生设想在太空中的飞船里进行的高中物理部分实验，可行的是(  )

A．用悬挂钩码法探究弹簧弹力和伸长的关系

B．用弹簧秤验证力的平行四边形定则

C．研究平抛物体的运动

D．利用自由落体运动验证机械能守恒定律

某星球的质量约为地球质量的8倍，半径约为地球半径的2倍。已知地球的第一宇宙速度为7.9 km/s，则航天器在该星球表面附近绕星球做匀速圆周运动的速度大小约为多少？

质量为100 kg行星探测器从某行星表面竖直发射升空，发射时发动机推力恒定，发射升空后8 s末，发动机突然间发生故障而关闭，探测器从发射到落回出发点全过程的速度图象如图所示。已知该行星半径是地球半径的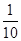，地球表面重力加速度为10m/s²，该行星表面没有大气，不考虑探测器总质量的变化。求：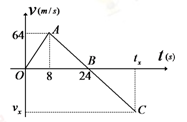

（1）探测器发动机推力大小；
（2）该行星的第一宇宙速度大小。

科学家对银河系中心附近的恒星 $S2$ 进行了多年的持续观测，给出1994年到2002年间 $S2$ 的位置如图所示。科学家认为 $S2$ 的运动轨迹是半长轴约为1000AU （太阳到地球的距离为 $1\mathit{AU}$ ）的椭圆，银河系中心可能存在超大质量黑洞。这项研究工作获得了2020年诺贝尔物理学奖。若认为 $S2$ 所受的作用力主要为该大质量黑洞的引力，设太阳的质量为 $M$ ，可以推测出该黑洞质量约为（　　）

A．

$4\times 10^{4}M$

B．

$4\times 10^{6}M$

C．

$4\times 10^{8}M$

D．

$4\times 10^{10}M$

从星球表面发射的物体能脱离星球的引力束缚不再绕星球运行所信的最小速度称为第二宇宙速度。星球的第二宇宙速度v₂与第一宇宙速度v₁的关系是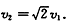；已知某星球的半径为r，它表面的重力加速度为地球表面重力加速度g的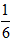．不计其他星球的影响，则该星球的第二宇宙速度为

地球赤道上的物体随地球自转的向心加速度为，第一宇宙速度为，地球半径为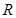，同步卫星离地心距离为，运行速率为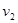，向心加速度为，则

A．	B．
C．	D．

如图所示，A是地球的同步卫星．另一卫星B的圆形轨道位于赤道平面内，离地面高度为h.已知地球半径为R，地球自转角速度为ω0，地球表面的重力加速度为g，O为地球中心．

(1)求卫星B的运行周期．
(2)如卫星B绕行方向与地球自转方向相同，某时刻A、B两卫星相距最近(O、B、A在同一直线上)，则至少经过多长时间，它们还能相距最近？

已知地球同步卫星的轨道半径约为地球半径的6.6倍．一飞行器绕地球做匀速圆周运动的周期为3小时。若地球半径为R，则该飞行器绕地心飞行的轨道半径最接近

A．0.83R

B．1.7R

C．1.9R

D．3.3R