高中物理万有引力定律及其应用选择题

人造卫星绕地球只受地球的引力，做匀速圆周运动，其轨道半径为r，线速度为v，周期为T。为使其周期变为8T，可采用的方法有

A．保持轨道半径不变，使线速度减小为v/8

B．逐渐减小卫星质量，使轨道半径逐渐增大为4r

C．逐渐增大卫星质量，使轨道半径逐渐增大为8r

D．保持线速度不变v，将轨道半径增加到8r

据报道，美国和俄罗斯的两颗卫星在太空相撞，相撞地点位于西伯利亚上空500英里(约805公里)．相撞卫星的碎片形成太空垃圾，并在卫星轨道附近绕地球运转，国际空间站的轨道在相撞事故地点下方270英里(434公里)．若把两颗卫星和国际空间站的轨道都看做圆形轨道，以下关于上述报道的说法正确的是

A．这两颗相撞卫星在同一轨道上

B．这两颗相撞卫星的周期、向心加速度大小一定相等

C．两相撞卫星的运行速度均大于国际空间站的速度

D．两相撞卫星的运行周期均大于国际空间站的运行周期

理论研究表明第二宇宙速度是第一宇宙速度的倍。火星探测器悬停在距火星表面高度为h处时关闭发动机，做自由落体运动，经时间t落到火星表面。已知引力常量为G，火星的半径为R。若不考虑火星自转的影响，要使探测器脱离火星飞回地球，则探测器从火星表面的起飞速度至少为

A．

B．

C．11.2km/s

D．7.9km/s

如图所示，太阳和地球组成“日地双星系统”，两者绕共同的圆心点（图中未画出）做周期相同的圆周运动．数学家拉格朗日发现，处在拉格朗日点（如图所示）的航天器在太阳和地球引力的共同作用下可以绕“日地双星系统”的圆心点做周期相同的圆周运动，从而使日、地、航天器三者在太空的相对位置保持不变．不考虑航天器对日地双星系统的影响，不考虑其它天体对该系统的影响．已知：太阳质量为，地球质量为，太阳与地球球心距离为．则下列说法正确的是

A．位于拉格朗日点的绕点稳定运行的航天器，其向心加速度小于地球的向心加速度

B．日地双星系统的周期为

C．圆心点在太阳和地球的连线上，距离太阳和地球球心的距离之比等于太阳和地球的质量之比

D．拉格朗日点距地球球心的距离满足关系式

假设有一载人宇宙飞船在距地面高度为4200km 的赤道上空绕地球做匀速圆周运动，地球半径约为6400km，地球同步卫星距地面高度为36000km，宇宙飞船和地球同步卫星绕地球同向运动，每当二者相距最近时，宇宙飞船就向同步卫星发射信号，然后再由同步卫星将信号发送到地面接收站，某时刻二者相距最远，从此刻开始，在一昼夜的时间内，接收站共接收到信号的次数为  （   ）

A．4次

B．6次

C．7次

D．8次

长期以来“卡戎星”被认为是冥王星唯一的卫星，它的公转轨道半径r₁≈2.0×10⁴km，公转周期T₁≈6天。2006年3月，天文学家新发现两颗冥王星的小卫星，其中一颗的公转轨道半径r₂≈4.8×10⁴km，取，则它的公转周期T₂最接近于 （    ）

A．11天

B．23天

C．35天

D．83天

2013年12月2日凌晨2时17分，“嫦娥三号”由“长征三号乙”运载火箭成功送入太空，经过一系列的调控和变轨，“嫦娥三号”最终顺利降落在月球表面，如图所示．“嫦娥三号”在地月转移轨道的P点调整后进入环月圆形轨道1，进一步调整后进入环月椭圆轨道2．有关“嫦娥三号”下列说法正确的是（　　）

A．在P点由轨道1进入轨道2需要减速

B．在地球上的发射速度一定大于第二宇宙速度

C．在轨道2经过P点时速度大于Q点速度

D．分别由轨道1与轨道2经P点时，向心加速度相同

太阳系个行星几乎在同一平面内沿同一方向绕太阳做圆周运动，当地球恰好运行到某个行星和太阳之间，且三者几乎成一条直线的现象，天文学成为"行星冲日"据报道，2014年各行星冲日时间分别是：1月6日，木星冲日，4月9日火星冲日，6月11日土星冲日，8月29日，海王星冲日，10月8日，天王星冲日，已知地球轨道以外的行星绕太阳运动的轨道半径如下表所示，则下列判断正确的是：（）

	地球	火星	木星	土星	天王星	海王星
轨道半径（AU）	1.0	1.5	5.2	9.5	19	30

A．	各点外行星每年都会出现冲日现象
B．	在2015年内一定会出现木星冲日
C．	天王星相邻两次的冲日的时间是土星的一半
D．	地外行星中海王星相邻两次冲日间隔时间最短

两个星球组成双星，它们在相互之间的引力作用下，绕连线上的某点做周期相同的匀速圆周运动．现测得两星中心距离为L，其运动周期为Ｔ，万有引力常量为G，则两星各自的圆周运动半径与其自身的质量成           （填“正比”或者“反比”）；两星的总质量为             。

教科版高中物理教材必修2中介绍, ,亚当斯通过对行星“天王星”的长期观察发现，其实际运行的轨道与圆轨道存在一些偏离，且每隔时间t发生一次最大的偏离。亚当斯利用牛顿发现的万有引力定律对观察数据进行计算, 认为形成这种现象的原因可能是天王星外侧还存在着一颗未知行星（后命名为海王星），它对天王星的万有引力引起其轨道的偏离。由于课本没有阐述其计算的原理，这极大的激发了树德中学天文爱好社团的同学的探索热情，通过集体研究，最终掌握了亚当斯当时的计算方法：设其（海王星）运动轨道与天王星在同一平面内，且与天王星的绕行方向相同，天王星的运行轨道半径为R，周期为T，并认为上述最大偏离间隔时间t就是两个行星相邻两次相距最近的时间间隔，并利用此三个物理量推导出了海王星绕太阳运行的圆轨道半径，则下述是海王星绕太阳运行的圆轨道半径表达式正确的是（  ）

A．

B．

C．

D．

假设月球半径为R，月球表面的重力加速度为g₀。如图所示，飞船首先沿距月球表面高度为3R的圆轨道I运动，到达轨道的A点时点火变轨进入椭圆轨道II，到达轨道II的近月点B再次点火进入近月轨道III(轨道半径可近似当做R)绕月球做圆周运动。下列判断正确的是（  ）

A．飞船在轨道I上的运行速率为

B．飞船在轨道III绕月球运动一周所需的时间为

C．飞船在A点点火变轨的瞬间，速度减小

D．飞船在A点的线速度大于在B点的线速度

已知引力常量G和下列各组数据，能计算出地球质量的是 （   ）

A．地球绕太阳运行的周期及地球离太阳的距离

B．人造地球卫星在地面附近运行的周期和轨道半径

C．月球绕地球运行的周期及月球的半径

D．若不考虑地球自转，已知地球的半径及地球表面的重力加速度

探月热方兴未艾，我国研制的月球卫星“嫦娥一号”、“嫦娥二号”均已发射升空，“嫦娥三号”于2013年发射升空。假设“嫦娥三号”在地球表面的重力为G₁，在月球表面的重力为G₂；地球与月球均视为球体，其半径分别为R₁、R₂；地球表面重力加速度为g。则

A．月球表面的重力加速度为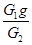

B．月球与地球的质量之比为

C．月球卫星与地球卫星分别绕月球表面附近与地球表面附近运行的速度之比为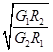

D．“嫦娥三号”环绕月球表面附近做匀速圆周运动的周期为

宇宙间存在一些离其他恒星较远的三星系统，其中有一种三星系统如图所示，三颗质量相等的星球位于等边三角形的三个顶点上，任意两颗星球的距离均为R，并绕其中心O做匀速圆周运动．忽略其他星球对它们的引力作用，引力常量为G，以下对该三星系统的说法正确的是   (　　)．

A．每颗星球做圆周运动的半径都等于R

B．每颗星球做圆周运动的加速度与三颗星球的质量无关

C．每颗星球做圆周运动的周期为T＝2πR

D．每颗星球做圆周运动的线速度v＝2

设地球是一质量分布均匀的球体，O为地心．已知质量分布均匀的球壳对壳内物体的引力为零．在下列四个图中，能正确描述x轴上各点的重力加速度g的分布情况的是(　　)．