若一均匀球形星体的密度为 ,引力常量为 ,则在该星体表面附近沿圆轨道绕其运动的卫星的周期是
| A. |
|
B. |
|
C. |
|
D. |
|
“嫦娥一号”卫星开始绕地球做椭圆轨道运动,经过变轨、制动后,成为一颗绕月球做圆轨道运动的卫星.设卫星距月球表面的高度为h,做匀速圆周运动的周期为T .已知月球半径为R,引力常量为G,其中R为球的半径。求:
(1)月球的质量M及月球表面的重力加速度g;
(2)在距月球表面高度为h的地方( ),将一质量为m的小球以v0的初速度水平抛出,求落地瞬间月球引力对小球做功的瞬时功率P.
),将一质量为m的小球以v0的初速度水平抛出,求落地瞬间月球引力对小球做功的瞬时功率P.
金星和木星都绕太阳做匀速圆周运动,木星绕太阳的公转周期是金星绕太阳的公转周期的
20倍,那么金星和木星绕太阳运行的线速度大小之比约为
A.2 |
B.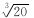 |
C.400 | D. |
我国的月球探测计划“嫦娥工程”分为“绕、落、回”三步。“嫦娥三号”的任务是“落”。2013年12月2日,“嫦娥三号”发射,经过中途轨道修正和近月制动之后,“嫦娥三号”探测器进入绕月的圆形轨道I。12月12日卫星成功变轨,进入远月点P、近月点Q的椭圆形轨道II,如图所示。2013年12月14日,“嫦娥三号”探测器在Q点附近制动,由大功率发动机减速,以抛物线路径下降到距月面100米高处进行30s悬停避障,之后再缓慢竖直下降到距月面高度仅为数米处,为避免激起更多月尘,关闭发动机,做自由落体运动,落到月球表面。
已知引力常量为G,月球的质量为M,月球的半径为R,“嫦娥三号”在轨道I上运动时的质量为m,P、Q点距月球表面的高度分别为h1、h2。
(1)求“嫦娥三号”在圆形轨道I上运动的速度大小;
(2)已知“嫦娥三号”与月心的距离为r时,引力势能为 (取无穷远处引力势能为零),其中m为此时“嫦娥三号”的质量。若“嫦娥三号”在轨道II上运动的过程中,动能和引力势能相互转化,它们的总量保持不变。已知“嫦娥三号”经过Q点的速度大小为v,请根据能量守恒定律求它经过P点时的速度大小;
(取无穷远处引力势能为零),其中m为此时“嫦娥三号”的质量。若“嫦娥三号”在轨道II上运动的过程中,动能和引力势能相互转化,它们的总量保持不变。已知“嫦娥三号”经过Q点的速度大小为v,请根据能量守恒定律求它经过P点时的速度大小;
我国“神舟”五号飞船于2003年l0月15日在酒泉航天发射场由长征二号F运载火箭成功发射升空,若长征二号F运载火箭和飞船起飞时总质量为1.0×105kg,起飞推动力为3.0×106N,运载火箭发射塔高160m,试问:(g=10m/s2)
(1)运载火箭起飞时的加速度为多大?
(2)假如运载火箭起飞时推动力不变,忽略一切阻力和运载火箭质量的变化,试确定运载火箭需经多长时间才能飞离发射塔?
(3)这段时间内飞船中的宇航员承受了多大的压力?(设宇航员的质量为65kg)
我国的“探月工程”计划将于2017年宇航员登上月球。若宇航员登上月球后,在距离月球水平表面h高度处,以初速度v0水平拋出一个小球,测得小球从抛出点到落月点的水平距离s。求:
(1)月球表面重力加速度 的大小;
的大小;
(2)小球落月时速度v的大小。
火星和木星沿各自的椭圆轨道绕太阳运行,根据开普勒行星运动定律可知
| A.太阳位于木星运行轨道的中心 |
| B.火星和木星绕太阳运行速度的大小始终相等 |
| C.火星与木星公转周期之比的平方等于它们轨道半长轴之比的立方 |
| D.相同时间内,火星与太阳连线扫过的面积等于木星与太阳连接扫过的面积 |
质量为m的人造地球卫星与地心的距离为r时,引力势能可表示为Ep=﹣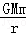 ,其中G为引力常量,M为地球质量.该卫星原来在半径为R1的轨道上绕地球做匀速圆周运动,由于受到极稀薄空气的摩擦作用,飞行一段时间后其圆周运动的半径变为R2,此过程中因摩擦而产生的热量为( )
,其中G为引力常量,M为地球质量.该卫星原来在半径为R1的轨道上绕地球做匀速圆周运动,由于受到极稀薄空气的摩擦作用,飞行一段时间后其圆周运动的半径变为R2,此过程中因摩擦而产生的热量为( )
A.GMm(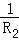 ﹣ ﹣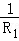 ) ) |
B.GMm(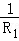 ﹣ ﹣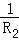 ) ) |
C.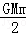 ( (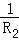 ﹣ ﹣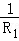 ) ) |
D.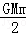 ( (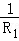 ﹣ ﹣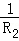 ) ) |
2017年4月,我国成功发射的天舟一号货运飞船与天宫二号空间实验室完成了首次交会对接,对接形成的组合体仍沿天宫二号原来的轨道(可视为圆轨道)运动。与天宫二号单独运行时相比,组合体运行的( )
| A. |
周期变大 |
B. |
速率变大 |
C. |
动能变大 |
D. |
向心加速变大 |
2019年1月,我国嫦娥四号探测器成功在月球背面软着陆,在探测器"奔向"月球的过程中,用h表示探测器与地球表面的距离,F表示它所受的地球引力,能够描F随h变化关系的图像是( )
A. 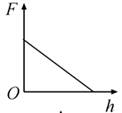 B.
B. 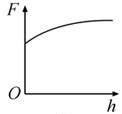
C. 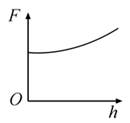 D.
D. 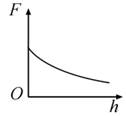
在星球
上将一轻弹簧竖直固定在水平桌面上,把物体P轻放在弹簧上端,P由静止向下运动,物体的加速度a与弹簧的压缩量x间的关系如图中实线所示。在另一星球N上用完全相同的弹簧,改用物体Q完成同样的过程,其
关系如图中虚线所示,假设两星球均为质量均匀分布的球体。已知星球M的半径是星球N的3倍,则( )

A.M与N的密度相等
B.Q的质量是P的3倍
C.Q下落过程中的最大动能是P的4倍
D.Q下落过程中弹簧的最大压缩量是P的4倍
甲、乙两颗人造卫星质量相等,均绕地球做圆周运动,甲的轨道半径是乙的2倍。下列应用公式进行的推论正确的有
| A. |
由 可知,甲的速度是乙的 倍 |
| B. |
由 可知,甲的向心加速度是乙的2倍 |
| C. |
由 可知,甲的向心力是乙的 |
| D. |
由 可知,甲的周期是乙的 倍 |
2014年12月31日,搭载“风云二号”08星的运载火箭在西昌卫星发射中心点火发射。发射过程中“风云二号”08星的某一运行轨道为椭圆轨道,周期为T0,如图所示。则( )
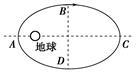
| A.“风云二号”08星的发射速度小于第一宇宙速度 |
| B.“风云二号”08星在A→B→C的过程中,速率逐渐变大 |
C.“风云二号”08星在A→B过程所用的时间小于 |
| D.“风云二号”08星在B→C→D的过程中,万有引力对它先做正功后做负功 |
在万有引力定律研究太阳系中的行星围绕太阳运动时,我们可以根据地球的公转周期,求出地球的质量.在运算过程中,采用理想化方法,把太阳和地球看成质点,还做了 和 的简化处理.有一人造天体飞临某个行星,并进入该行星的表面圆轨道,测出该天体绕行星运行一周所用的时间为T,则这颗行星的密度是 .
黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成。两星视为质点,不考虑其它天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示。引力常量为G,由观测能够得到可见星A的速率v和运行周期T。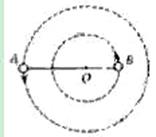
(1)可见星A所受暗星B的引力 可等效为位于O点处质量为
可等效为位于O点处质量为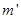 的星体(视为质点)对它的引力,设A和B的质量分别为
的星体(视为质点)对它的引力,设A和B的质量分别为 、
、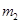 ,试求
,试求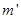 (用
(用 、
、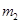 表示);
表示);
(2)求暗星B的质量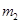 与可见星A的速率v、运行周期T和质量
与可见星A的速率v、运行周期T和质量 之间的关系式;
之间的关系式;
(3)恒星演化到末期,如果其质量大于太阳质量 的2倍,它将有可能成为黑洞。若可见星A的速率v=2.7×105m/s,运行周期T=4.7π×104s,质量m1=6
的2倍,它将有可能成为黑洞。若可见星A的速率v=2.7×105m/s,运行周期T=4.7π×104s,质量m1=6 ,试通过估算来判断暗星B有可能是黑洞吗?(G=6.67×10-11N·m2/kg2,ms=2.0×1030kg)
,试通过估算来判断暗星B有可能是黑洞吗?(G=6.67×10-11N·m2/kg2,ms=2.0×1030kg)