高中物理匀速圆周运动计算题

一台走动准确的时钟，其秒针、分针、时针的长度之比为l₁∶l₂∶l₃＝3∶2∶1，试求：
(1)秒针、分针、时针转动的角速度之比．
(2)秒针、分针、时针针尖的线速度大小之比．

2010年温哥华冬奥会双人滑比赛中，申雪、赵宏博拿到中国花样滑冰史上首枚冬奥会金牌，如图所示，赵宏博(男)以自己为转轴拉着申雪(女)做匀速圆周运动，转速为30r/min.申雪的脚到转轴的距离为1.6m.求：

(1)申雪做匀速圆周运动的角速度；
(2)申雪的脚运动速度的大小．

如图所示，M是水平放置的半径足够大的圆盘，可绕过其圆心的竖直轴OO’匀速转动，在圆心O正上方h处有一个正在间断滴水的容器，每当一滴水落在盘面时恰好下一滴水离开滴口。某次一滴水离开滴口时，容器恰好开始水平向右做速度为v的匀速直线运动，将此滴水记作第一滴水。不计空气阻力，重力加速度为g。求：

（1）相邻两滴水下落的时间间隔；
（2）第二滴和第三滴水在盘面上落点之间的距离最大可为多少？；

(6分)如图所示，在以角速度ω=2rad/s匀速转动的水平圆盘上，放一质量m=5kg的滑块，滑块离转轴的距离r=0.2m，滑块跟随圆盘一起做匀速圆周运动（二者未发生相对滑动）．求：

（1）滑块运动的线速度大小；
（2）滑块受到静摩擦力的大小和方向．
（3）滑块跟随圆盘运动一周过程中静摩擦力所做的功．

如图所示，图甲为游乐场的悬空旋转椅，我们把这种情况抽象为图乙的模型：一质量m = 40kg的小球通过长L=12.5m的轻绳悬于竖直面内的直角杆上，水平杆长
L′= 7.5m。整个装置绕竖直杆转 动，绳子与竖直方向成θ角。求：

(1) 要使θ =37°，试求该装置必须以多大角速度转动才行？
（2）此时绳的张力是多大？（g = 10m/s²，sin37°= 0.6，cos37°= 0.8）

长L＝0.5 m的轻杆，其一端连接着一个零件A，A的质量m＝１kg. 现让A在竖直平面内绕O点做匀速圆周运动，如图所示．在A通过最高点时，求下列两种情况下A对杆的作用力：

(1)A的速率为 ２m/s；
(2)A的速率为３m/s.(g＝10 m/s²)

用长为L的细绳栓住一个质量为m的小球，如图所示，当小球在水平面内做匀速圆周运动时，细绳与竖直方向成角，求小球做匀速圆周运动的周期及细绳对小球的拉力。

如图所示，两平行金属板间距为d，电势差为U，板间电场可视为匀强电场；金属板下方有一磁感应强度为B的匀强磁场。带电量为+q、质量为m的粒子，由静止开始从正极板出发，经电场加速后射出，并进入磁场做匀速圆周运动。忽略重力的影响，求：

（1）匀强电场的电场强度E的大小。
（2）粒子从电场射出时速度v的大小。
（3）粒子在磁场中做匀速圆周运动的半径R。

一物体在水平面内沿半径 R=" 0.20" m的圆形轨道做匀速圆周运动，线速度V=0.2m/s，试求：（1）它的向心加速度为多少m/s²？（2）它的角速度为多少 rad/s？

如图所示，长为R的轻质杆（质量不计），一端系一质量为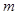的小球（球大小不计），绕杆的另一端O在竖直平面内做匀速圆周运动，若小球最低点时，杆对球的拉力大小为1.5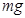，求：

①小球最低点时的线速度大小？
②小球通过最高点时，杆对球的作用力的大小及方向？
③小球以多大的线速度运动，通过最高处时杆对球不施力？

如图所示，是双人花样滑冰运动中男运动员拉着女运动员做圆锥摆运动的精彩场面．若女运动员伸直的身体与竖直方向的夹角为θ，质量为m，转动过程中女运动员的重心做匀速圆周运动的半径为r，忽略女运动员受到的摩擦力，重力加速度为g，求

（1）当女运动员对冰面的压力为其重力的1/2时，男运动员的拉力大小及两人转动的周期；
（2）当女运动员刚要离开冰面时，男运动员的拉力大小及两人转动的周期．

如图所示，有一水平放置的圆盘，上面水平放一劲度系数为的弹簧，弹簧的一端固定于轴上，另一端连接一质量为的物体A，物体与盘面间的动摩擦因数为，开始时弹簧未发生形变，长度为，设最大静摩擦力等于滑动摩擦力。

则：（1）盘的转速n₀多大时，物体A开始滑动？
（2）当转速达到2n₀时，弹簧的伸长量是多少？

如图所示，轻杆的一端用铰链固定在竖直转轴OO′上的O端，另一端固定一小球，轻杆可在竖直平面内自由转动，当转轴以某一角速度匀速转动时，小球在水平面内做匀速圆周转动，此时轻杆与竖直转轴OO′的夹角为37°．已知转轴O端距离水平地面的高度为h，轻杆长度为L，小球的质量为m，重力加速度为g，取sin37°≈0.6，cos37°≈0.8，求：

（1）小球做匀速圆周运动的线速度v．
（2）若某时刻小球从轻杆上脱落，小球的落地点到转轴的水平距离d．
（3）若缓慢增大转轴的转速，求轻杆与转轴的夹角从37°增加到53°的过程中，轻杆对小球所做的功W．

一辆质量m=2.0×10³kg的汽车，经过半径r=50m的水平弯路．则：
（1）当汽车的速度v=10m/s时，受到的向心力为多大？
（2）若汽车轮胎与路面间的最大静摩擦力F_m=9.0×10³N，为了使这辆车通过此段弯路时不发生侧滑，行驶的最大速度为多大？

质点P以O为圆心做半径为R的匀速圆周运动，如图所示，周期为T。当P经过图中D点时，有一质量为m的另一质点Q受到力F的作用从静止开始作匀加速直线运动。为使P、Q两质点在某时刻的速度相同，则F的大小应满足什么条件？